设隐式单步法公式 yn+1＝yn＋[4f(χn yn)＋2f(χn+1 yn+1)＋hf′(χn y
设隐式单步法公式 yn+1＝yn＋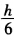
[4f(χn，yn)＋2f(χn+1，yn+1)＋hf′(χn，yn)] 证明：它是三阶方法。
请帮忙给出正确答案和分析，谢谢！
参考解答
432***102
2024-11-17 08:51:34
正确答案：设yn＝y(χn)则y′(χn)＝f(χnyn)y〞(χn)＝f′(χnyn)及f(χn+1yn+1)＝f(χn+1y(χn+1))＝y′(χn+1)由Taylor展式 y′(χ)＝y′(χ)＋hy〞(χ)＋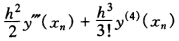
＋… 将其代入公式有
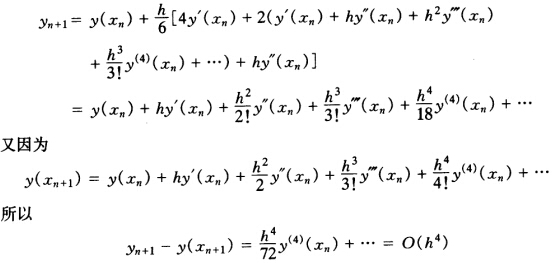故该方法为三阶。
设yn＝y(χn),则y′(χn)＝f(χn,yn),y〞(χn)＝f′(χn,yn),及f(χn+1,yn+1)＝f(χn+1,y(χn+1))＝y′(χn+1)由Taylor展式y′(χ)＝y′(χ)＋hy〞(χ)＋＋…将其代入公式有故该方法为三阶。
相似问题
设初值问题应用Adams预估一校正方法解初值问题 取h＝0．1计算其数值解 并与精确解比较。应用Ad
设初值问题应用Adams预估一校正方法解初值问题 取h＝0．1计算其数值解，并与精确解比较。应用Adams预估一校正方法解初值问题 取h＝0．1计算其数值解
设χ∈Rn (1)‖χ‖∞≤‖χ‖1≤n‖χ‖∞； (2)‖χ‖∞≤‖χ‖2≤设线性方程组 已知一
设χ∈Rn， (1)‖χ‖∞≤‖χ‖1≤n‖χ‖∞； (2)‖χ‖∞≤‖χ‖2≤设线性方程组 已知一个近似解χ(0)＝(－设线性方程组 已知一个近似解χ(0)＝(
设f(χ)＝sinχ的函数表如下： 设f(χ)∈C5[a b] 求一不高于4次的插值多项式P(χ)
设f(χ)＝sinχ的函数表如下： 设f(χ)∈C5[a，b]，求一不高于4次的插值多项式P(χ)，满足 f(0)＝P(0)设f(χ)∈C5[a，b]，求一不高于4次的插值多项式P(
用已知浓度的NaOH标准溶液 滴定同浓度的弱酸 Ka越大 则( )。A．消耗NaOH的体积越大B．滴
用已知浓度的NaOH标准溶液，滴定同浓度的弱酸，Ka越大，则( )。A．消耗NaOH的体积越大B．滴定突跃越大C．滴定突跃越小D．指示剂颜色变化相同请帮忙给出
设三阶Hilbert矩阵 试用带位移的单步QR方法求下列矩阵的全部特征值。试用带位移的单步QR方法求
设三阶Hilbert矩阵 试用带位移的单步QR方法求下列矩阵的全部特征值。试用带位移的单步QR方法求下列矩阵的全部特征值。 请帮忙给出正确答案和分析，谢谢！
