设定积分用Gauss－Legendre求积公式计算定积分 (1)I＝∫－11 (n＝3 4 5)；
设定积分用Gauss－Legendre求积公式计算定积分 (1)I＝∫－11，(n＝3，4，5)； (2)I＝∫0πcosχdχ，(
用Gauss-Legendre求积公式计算定积分 (1)I＝∫-11，(n＝3，4，5)； (2)I＝∫0πcosχdχ，(n＝4，5)，(注：对χ∈[a，b]，令χ＝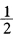
(b－a)t＋
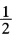(a＋b)，则t∈[－1，1]，真值I＝－
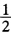(1＋eπ＝－12．0703463…)。
请帮忙给出正确答案和分析，谢谢！
参考解答
456***102
2024-11-17 11:41:52
正确答案：×
(1)Gauss-Legendre求积公式为∫-11f(χ)dχ≈Akf(χk)其中Ak＝,Pn(χ)为Lelgendre多项式,于是对n＝3,4,5计算得I≈I4＝0．3478548451×(f(0．8611363116)＋f(－0．8611363116))＋0．6521451549×(f(0．3399810436)＋f(－0．3399810436))＝2．35040209214208I≈I5＝0．23692688506×(f(0．9061798459)＋f(－0．9061798459))＋0．4786286705×(f(0．5384693101)＋f(－0．5384693101))＋0．5688888889f(0)＝2．35040238646432I≈I6＝0．1713244924×(f(0．9324695142)＋f(－0．9324695142))＋0．3607615730×(f(0．6612093865)＋f(－0．6612093865))＋0．4679139346×(f(0．2386191861)＋f(－0．2386191861))＝2．35040238730516(2)令χ＝,则I＝I≈I5＝0．23692688506×(f(0．9061798459)＋f(－0．9061798459))＋0．4786286705×(f(0．5384693101)＋f(－0．5384693101))＋0．5688888889×f(0)＝－12．0703285353647I≈I6＝0．1713244924×(f(0．9324695142)＋f(－0．9324695142))＋0．3607615730×(f(0．6612093865)＋f(－0．6612093865))＋0．4679139346×(f(0．2386191861)＋f(－0．2386191861))＝－12．0703463317111
相似问题
试用Gauss—Jordan消去法求下列矩阵的逆矩阵。 请帮忙给出正确答案和分析 谢谢！
试用Gauss—Jordan消去法求下列矩阵的逆矩阵。 请帮忙给出正确答案和分析，谢谢！
设三阶Hilbert矩阵 (1)试用幂法和反幂法求矩阵H3的按模最大和最小特征值及相应的特征向量。
设三阶Hilbert矩阵 (1)试用幂法和反幂法求矩阵H3的按模最大和最小特征值及相应的特征向量。 (2)试用Jacobi法求矩阵H3的全部特征值和特征向量。请帮忙
设A为n阶实对称矩阵 其特征值为λ1≥λ2≥…≥λn 相应的特征向量χ1 χ1 … χn 且组成规范
设A为n阶实对称矩阵，其特征值为λ1≥λ2≥…≥λn，相应的特征向量χ1，χ1，…，χn，且组成规范化正交向量组，证明： 请帮忙给出正确答案和分析，谢谢！
Hilbert矩阵设线性方程组 试用Jacobi迭代法及GausS－Seidel迭代法求方程组的解设
Hilbert矩阵设线性方程组 试用Jacobi迭代法及GausS－Seidel迭代法求方程组的解设线性方程组 试用Jacobi迭代法及GausS-Seidel迭代法求方程组的解请帮忙
试用n＝1 2 3 4的Newton－cotes求积公式计算定积分I＝用Gauss－Legendre
试用n＝1，2，3，4的Newton－cotes求积公式计算定积分I＝用Gauss－Legendre求积公式(取n＝4)计算定积分eχ用Gauss-Legendre求积公式(取n＝4)计算定积分e
