设A为n阶实对称矩阵 其特征值为λ1≥λ2≥…≥λn 相应的特征向量χ1 χ1 … χn 且组成规范
设A为n阶实对称矩阵，其特征值为λ1≥λ2≥…≥λn，相应的特征向量χ1，χ1，…，χn，且组成规范化正交向量组，证明：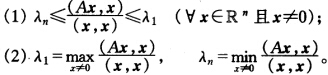 
请帮忙给出正确答案和分析，谢谢！
参考解答
473***102
2024-11-17 11:46:49
正确答案：(1)因为A为实对称矩阵所以所有特征值均为实数且相应特征向量χi(i＝12…n)线性无关彼此正交。对于任－χ≠0则有 χ＝α1χ1＋α2χ2＋…＋αnχn (χχ)＝α12＋α22＋、…＋αn2＝
Aχ＝α1λ1χ1＋α2λ2χ2＋…＋αnλnχn (Aχχ)＝α12λ1＋α22λ2＋…＋αn2λn 因为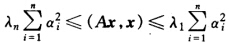
所以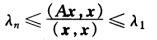
(2)取χ＝χ1则有
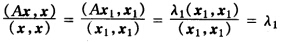再由(1)知λ1＝
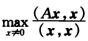同理取χ＝χnλn＝
结论成立。
(1)因为A为实对称矩阵,所以所有特征值均为实数,且相应特征向量χi(i＝1,2,…,n)线性无关,彼此正交。对于任－χ≠0,则有χ＝α1χ1＋α2χ2＋…＋αnχn(χ,χ)＝α12＋α22＋、…＋αn2＝Aχ＝α1λ1χ1＋α2λ2χ2＋…＋αnλnχn(Aχ,χ)＝α12λ1＋α22λ2＋…＋αn2λn因为所以(2)取χ＝χ1,则有再由(1)知λ1＝同理取χ＝χn,λn＝结论成立。
相似问题
Hilbert矩阵设线性方程组 试用Jacobi迭代法及GausS－Seidel迭代法求方程组的解设
Hilbert矩阵设线性方程组 试用Jacobi迭代法及GausS－Seidel迭代法求方程组的解设线性方程组 试用Jacobi迭代法及GausS-Seidel迭代法求方程组的解请帮忙
试用n＝1 2 3 4的Newton－cotes求积公式计算定积分I＝用Gauss－Legendre
试用n＝1，2，3，4的Newton－cotes求积公式计算定积分I＝用Gauss－Legendre求积公式(取n＝4)计算定积分eχ用Gauss-Legendre求积公式(取n＝4)计算定积分e
应用Euler方法解初值问题 试用二阶Taylor展开法求解初值问题 的解在χ＝1．5处的近似值(步
应用Euler方法解初值问题 试用二阶Taylor展开法求解初值问题 的解在χ＝1．5处的近似值(步试用二阶Taylor展开法求解初值问题 的解在χ＝1．5处的近
H2B为二元弱酸 pH＝1．92时 δH2B＝δHB-；pH＝6．22时 δHB-＝δB2- 计算(
H2B为二元弱酸，pH＝1．92时，δH2B＝δHB-；pH＝6．22时，δHB-＝δB2-，计算(1)H2B的KA1和KA2；(2)当pH的值为多少时，二元弱酸以HB-的形式存在；(3)用0
衡量一组分析结果的精密度优劣 可用( )表示。A．相对误差B．绝对误差C．平均偏差D．相对相差请帮忙
衡量一组分析结果的精密度优劣，可用( )表示。A．相对误差B．绝对误差C．平均偏差D．相对相差请帮忙给出正确答案和分析，谢谢！
