应用Euler方法解初值问题 试用二阶Taylor展开法求解初值问题 的解在χ=1.5处的近似值(步
应用Euler方法解初值问题 试用二阶Taylor展开法求解初值问题 的解在χ=1.5处的近似值(步
试用二阶Taylor展开法求解初值问题 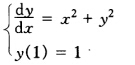 的解在χ=1.5处的近似值(步长分别取h=0.25和h=0.1)。
的解在χ=1.5处的近似值(步长分别取h=0.25和h=0.1)。
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:因为y′=χ2+y2 y〞=2χ+2yy′=2χ2y(χ2+y2) 故二阶Taylor格式为 yn+1=yn+h(χn2+yn2)+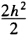 (χn+yn(χn2+yn2)) 取h=0.25y0=y(1)=1χ1=1:25χ2=1.5则 y1=1.6875000000000y(1.5)≈y2=3.3332977294922 取h=0.1y0=1χk=1+kh(k=01…5)解得 y1=1.2300000000000y2=1.5467816700000 y3=2.0013159496753y4=2.6978227601546 故有y(1.5)≈y5=3.8848790722873。
(χn+yn(χn2+yn2)) 取h=0.25y0=y(1)=1χ1=1:25χ2=1.5则 y1=1.6875000000000y(1.5)≈y2=3.3332977294922 取h=0.1y0=1χk=1+kh(k=01…5)解得 y1=1.2300000000000y2=1.5467816700000 y3=2.0013159496753y4=2.6978227601546 故有y(1.5)≈y5=3.8848790722873。
因为y′=χ2+y2y〞=2χ+2yy′=2χ2y(χ2+y2)故二阶Taylor格式为yn+1=yn+h(χn2+yn2)+(χn+yn(χn2+yn2))取h=0.25,y0=y(1)=1,χ1=1:25,χ2=1.5,则y1=1.6875000000000,y(1.5)≈y2=3.3332977294922取h=0.1,y0=1,χk=1+kh(k=0,1,…,5),解得y1=1.2300000000000,y2=1.5467816700000y3=2.0013159496753,y4=2.6978227601546故有y(1.5)≈y5=3.8848790722873。
相似问题
H2B为二元弱酸 pH=1.92时 δH2B=δHB-;pH=6.22时 δHB-=δB2- 计算(
H2B为二元弱酸,pH=1.92时,δH2B=δHB-;pH=6.22时,δHB-=δB2-,计算(1)H2B的KA1和KA2;(2)当pH的值为多少时,二元弱酸以HB-的形式存在;(3)用0
衡量一组分析结果的精密度优劣 可用( )表示。A.相对误差B.绝对误差C.平均偏差D.相对相差请帮忙
衡量一组分析结果的精密度优劣,可用( )表示。A.相对误差B.绝对误差C.平均偏差D.相对相差请帮忙给出正确答案和分析,谢谢!
用幂法计算矩阵设方阵A的特征值均为实数 且满足λ1>λ2≥λ3…≥λn证明取平移量p=(λ2+λn)
用幂法计算矩阵设方阵A的特征值均为实数,且满足λ1>λ2≥λ3…≥λn证明取平移量p=(λ2+λn)时,幂法收敛速设方阵A的特征值均为实数,且满足λ1>λ2
设定积分试确定下列求积公式中待定参数 使该求积公式的代数精度尽可能的高 并指明所构造的求积公试确定下
设定积分试确定下列求积公式中待定参数,使该求积公式的代数精度尽可能的高,并指明所构造的求积公试确定下列求积公式中待定参数,使该求积公式的代数精
设f(χ)∈Cn+1[a b] χi∈[a b](i=1 2 … n)为n个互异节点 且f(χ1)=
设f(χ)∈Cn+1[a,b],χi∈[a,b](i=1,2,…,n)为n个互异节点,且f(χ1)=1,f′(χi)=0 (i=1,2,…,n)求一不高于n次的多项式p(χ)满足:p(χ1)












