Hilbert矩阵讨论线性方程组 Jacobi迭代法及Gauss－Seidel迭代法的收敛性。讨论线
Hilbert矩阵讨论线性方程组 Jacobi迭代法及Gauss－Seidel迭代法的收敛性。
讨论线性方程组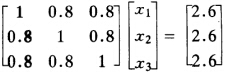 
Jacobi迭代法及Gauss－Seidel迭代法的收敛性。
请帮忙给出正确答案和分析，谢谢！
参考解答
432***102
2024-11-17 11:47:11
正确答案：线性方程组有唯一解χ*＝(111)T它的系数矩阵 A＝
是对称正定的所以Gauss-Seidel迭代法收敛。 又因为GJ＝J－D-1A＝I－A的特征值是λ1＝0．8λ2＝0．8λ3＝－1．6因此ρ(GJ)＝1．6＞1故知Jacobi迭代法不收敛。
线性方程组有唯一解χ*＝(1,1,1)T,它的系数矩阵A＝是对称正定的,所以Gauss-Seidel迭代法收敛。又因为GJ＝J－D-1A＝I－A的特征值是λ1＝0．8,λ2＝0．8,λ3＝－1．6,因此ρ(GJ)＝1．6＞1,故知Jacobi迭代法不收敛。
相似问题
设定积分用Gauss－Legendre求积公式计算定积分 (1)I＝∫－11 (n＝3 4 5)；
设定积分用Gauss－Legendre求积公式计算定积分 (1)I＝∫－11，(n＝3，4，5)； (2)I＝∫0πcosχdχ，(用Gauss-Legendre求积公式计算定积分 (1)I＝∫-1
试用Gauss—Jordan消去法求下列矩阵的逆矩阵。 请帮忙给出正确答案和分析 谢谢！
试用Gauss—Jordan消去法求下列矩阵的逆矩阵。 请帮忙给出正确答案和分析，谢谢！
设三阶Hilbert矩阵 (1)试用幂法和反幂法求矩阵H3的按模最大和最小特征值及相应的特征向量。
设三阶Hilbert矩阵 (1)试用幂法和反幂法求矩阵H3的按模最大和最小特征值及相应的特征向量。 (2)试用Jacobi法求矩阵H3的全部特征值和特征向量。请帮忙
设A为n阶实对称矩阵 其特征值为λ1≥λ2≥…≥λn 相应的特征向量χ1 χ1 … χn 且组成规范
设A为n阶实对称矩阵，其特征值为λ1≥λ2≥…≥λn，相应的特征向量χ1，χ1，…，χn，且组成规范化正交向量组，证明： 请帮忙给出正确答案和分析，谢谢！
Hilbert矩阵设线性方程组 试用Jacobi迭代法及GausS－Seidel迭代法求方程组的解设
Hilbert矩阵设线性方程组 试用Jacobi迭代法及GausS－Seidel迭代法求方程组的解设线性方程组 试用Jacobi迭代法及GausS-Seidel迭代法求方程组的解请帮忙
