考虑下列问题： 用共轭梯度法求解下列问题： (1)．取初始点x(1)=(4 4)T． (2)min

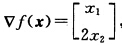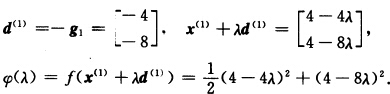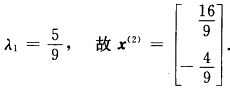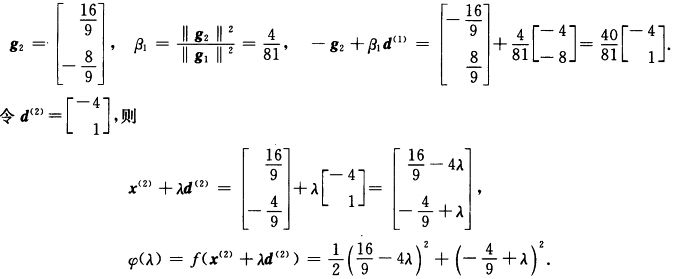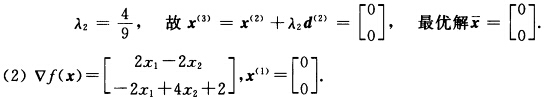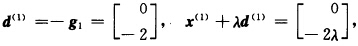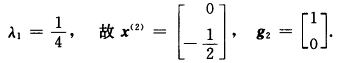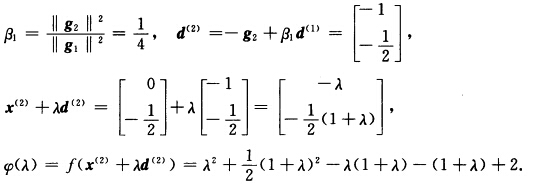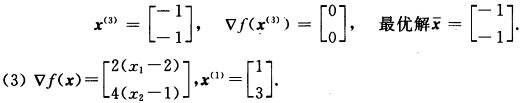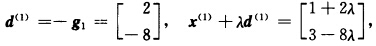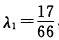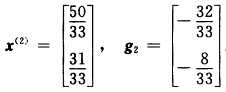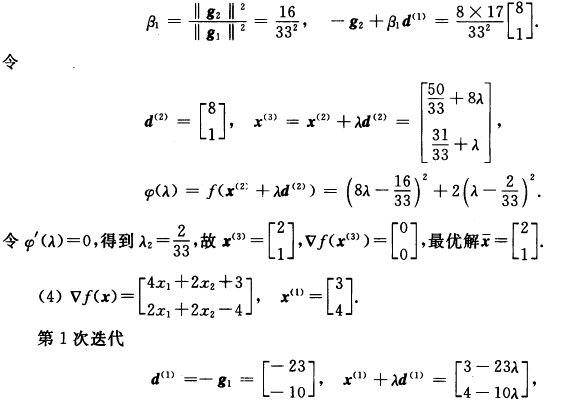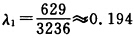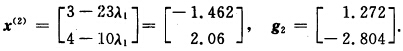正确答案：目标函数记作f(x)在点x^(k)处目标函数的梯度记作g_k=▽f(x^(k))． (1)搜索方向记作d^(k)．第1次迭代：令φ’(λ)=0．得到第2次迭代：令φ’(λ)=0得到第1次迭代：φ(λ)=f(x⁽¹⁾+λd⁽¹⁾)=8λ²一4λ+2．令φ’(λ)=0得到第2次迭代：令φ’(λ)=0得到λ₂=1故第1次迭代：φ(λ)=(2λ-1)²+2(2—8λ)²．令φ’(λ)=0得到故第2次迭代：φ(λ)=2(3—23λ)²+2(3—23λ)(4—10λ)+(4—10λ)²+3(3—23λ)一4(4—10λ)．令φ’(λ)=0得到故第2次迭代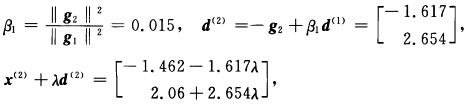： φ(λ)=2(一1．462—1．617λ)²+2(-1．462—1．617λ)(2．06+2．654λ) +(2．06+2．654λ)²+3(一1．462—1．617λ)一4(2．06+2．654λ)．令φ’(λ)=0即7．380λ-9．499=0得λ₂=1．287φ(λ)=f(x⁽¹⁾+λd⁽¹⁾)=2(2—4λ)²+2(2—4λ)(一2+16λ)+5(-2+16λ)²．令φ’(λ)=0解得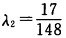于是得到
目标函数记作f(x),在点x(k)处目标函数的梯度记作gk=▽f(x(k))．(1)搜索方向记作d(k)．第1次迭代：令φ’(λ)=0．得到第2次迭代：令φ’(λ)=0,得到第1次迭代：φ(λ)=f(x(1)+λd(1))=8λ2一4λ+2．令φ’(λ)=0,得到第2次迭代：令φ’(λ)=0,得到λ2=1,故第1次迭代：φ(λ)=(2λ-1)2+2(2—8λ)2．令φ’(λ)=0,得到,故第2次迭代：φ(λ)=2(3—23λ)2+2(3—23λ)(4—10λ)+(4—10λ)2+3(3—23λ)一4(4—10λ)．令φ’(λ)=0,得到故第2次迭代：φ(λ)=2(一1．462—1．617λ)2+2(-1．462—1．617λ)(2．06+2．654λ)+(2．06+2．654λ)2+3(一1．462—1．617λ)一4(2．06+2．654λ)．令φ’(λ)=0,即7．380λ-9．499=0,得λ2=1．287,φ(λ)=f(x(1)+λd(1))=2(2—4λ)2+2(2—4λ)(一2+16λ)+5(-2+16λ)2．令φ’(λ)=0,解得于是得到