设χj=χ0+jh(j=0 1 2 … n) ωn(χ)=设χi(j=0 1 2 … n)为互异节点
设χj=χ0+jh(j=0,1,2,…,n),ωn(χ)=设χi(j=0,1,2,…,n)为互异节点,证明
设χi(j=0,1,2,…,n)为互异节点,证明 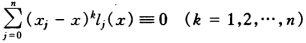
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:由于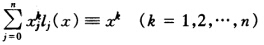 所以对任意k=12…n有
所以对任意k=12…n有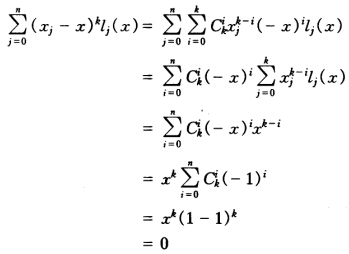 因此结论成立。
因此结论成立。
由于所以对任意k=1,2,…,n,有因此结论成立。
相似问题
设A∈Rn×n为对称正定矩阵 χ∈Rn ‖χ‖=设矩阵 试求‖A1‖2 ‖A2‖2 ρ(A1) ρ(
设A∈Rn×n为对称正定矩阵,χ∈Rn,‖χ‖=设矩阵 试求‖A1‖2,‖A2‖2,ρ(A1),ρ(A2)。设矩阵 试求‖A1‖2,‖A2‖2,ρ(A1),ρ(A2)。请帮忙给
若TNaOH/HCL=0.006000g/mL 求此标准溶液的浓度。请帮忙给出正确答案和分析 谢谢!
若TNaOH HCL=0.006000g/mL,求此标准溶液的浓度。请帮忙给出正确答案和分析,谢谢!
设线性方程组设A是对称正定矩阵 线性方程组Aχ=b经过Gauss顺序消元法一步后 A约化为A(2)=
设线性方程组设A是对称正定矩阵,线性方程组Aχ=b经过Gauss顺序消元法一步后,A约化为A(2)= 其设A是对称正定矩阵,线性方程组Aχ=b经过Gauss顺序消元
设线性方程组 中aii≠0(i=1 2) 证明:解此方程组的Jacobi迭代法和Gauss-Seid
设线性方程组 中aii≠0(i=1,2),证明:解此方程组的Jacobi迭代法和Gauss-Seidel迭代法同时收敛或同时发散,并给出收敛的充分必要条件。请帮忙给出正确
设用Gauss全主元消元法解方程组用Gauss全主元消元法解方程组请帮忙给出正确答案和分析 谢谢!
设用Gauss全主元消元法解方程组用Gauss全主元消元法解方程组请帮忙给出正确答案和分析,谢谢!












