设A为对称正定矩阵 解线性方程组Aχ＝b的迭代格式为 χ(k+1)＝χ(k)＋ω(b－Aχ(k))
设A为对称正定矩阵，解线性方程组Aχ＝b的迭代格式为 χ(k+1)＝χ(k)＋ω(b－Aχ(k)) (k＝0，1，2，…) 证明：当0＜ω＜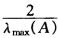
时，迭代法收敛。
请帮忙给出正确答案和分析，谢谢！
参考解答
420***102
2024-11-17 09:47:09
正确答案：迭代格式 χ(k+1)＝χ(k)＋ω(b－Aχ(k)) (k＝012…) 可改写为 χ(k+1)＝(I－ωA)χ(k)＋ωb (k＝012…) 即迭代矩阵为Gω＝I－ωA。 设λ为A的特征值由高等代数知μ＝1－ωλ是Gω的特征值。因为A是对称正定所以λ＞0因此有μmax＝1－ωλmin 又因为0＜ω＜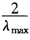
所以1－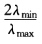
＜μmax＜1 即有－1＜μmax＜1 所以有ρ(Gω)＜1因此迭代法收敛。
迭代格式χ(k+1)＝χ(k)＋ω(b－Aχ(k))(k＝0,1,2,…)可改写为χ(k+1)＝(I－ωA)χ(k)＋ωb(k＝0,1,2,…)即迭代矩阵为Gω＝I－ωA。设λ为A的特征值,由高等代数知μ＝1－ωλ是Gω的特征值。因为A是对称正定,所以λ＞0,因此有μmax＝1－ωλmin又因为0＜ω＜,所以1－＜μmax＜1即有－1＜μmax＜1所以有ρ(Gω)＜1,因此迭代法收敛。
相似问题
设线性方程组Aχ＝b的系数矩阵为 其中a为实参数。证明：当＜a＜1时 G-S迭代法解方程组收敛。请
设线性方程组Aχ＝b的系数矩阵为 其中a为实参数。证明：当＜a＜1时，G-S迭代法解方程组收敛。请帮忙给出正确答案和分析，谢谢！
证明：基本插值多项式lj(χ)(j＝0 1 2 … n)是线性无关的。请帮忙给出正确答案和分析 谢谢
证明：基本插值多项式lj(χ)(j＝0，1，2，…，n)是线性无关的。请帮忙给出正确答案和分析，谢谢！
设A为严格对角占优矩阵 经过Gauss顺序消元法一步后 A约化为设P是正交矩阵 证明：‖PA‖F＝‖
设A为严格对角占优矩阵，经过Gauss顺序消元法一步后，A约化为设P是正交矩阵，证明：‖PA‖F＝‖AP‖F＝‖A‖F设P是正交矩阵，证明：‖PA‖F＝‖AP‖F＝‖
已知函数f(χ)＝lnχ和它的导数f′(χ)＝试求f(χ)＝ χ∈[0 1]上的一次最佳平方逼近多项
已知函数f(χ)＝lnχ和它的导数f′(χ)＝试求f(χ)＝，χ∈[0，1]上的一次最佳平方逼近多项式。试求f(χ)＝，χ∈[0，1]上的一次最佳平方逼近多项式。请
下列数据中 有效数字为二位的是( ) 有效数字是四位的是( )。A．pH＝11．03B．(CH+)＝
下列数据中，有效数字为二位的是( )，有效数字是四位的是( )。A．pH＝11．03B．(CH+)＝0．0800mol／LC．6000D．T(HCL／NaOH)＝0．1257g·mol-1请帮忙给出正确答案和分析，谢谢！
