设n阶矩阵 (1)求A的特征值和特征向量； (2)求可逆矩阵P 使得P－1AP为对角矩阵．请帮忙给

正确答案：(1)1° 当b≠0时A的特征值为λ₁＝1＋(n－1)bλ₂＝…＝λ_n＝1—b． 对λ₁＝1＋(n－1)bA的属于λ₁的全部特征向量为kξ₁＝k(111…1)^T． 对λ₂＝1－b故A的属于λ₂的全部特征向量为k₂ξ₂＋k₃ξ₃＋…＋k_nξ_n其中ξ₂＝(1－10…0)^Tξ₂＝(10－1…0)^T…ξ₂＝(100…－1)^T． 2° 当b＝0时特征值为λ₁＝…＝λ_n＝1任意非零列向量均为特征向量．(2)1° 当b≠0时A有n个线性无关的特征向量令P＝(ξ₁ξ₂…ξ_n)则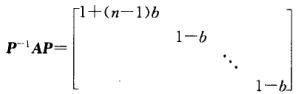 2° 当b＝0时A＝E对任意可逆矩阵P均有P^－1AP＝E．
(1)1°当b≠0时,A的特征值为λ1＝1＋(n－1)b,λ2＝…＝λn＝1—b．对λ1＝1＋(n－1)b,A的属于λ1的全部特征向量为kξ1＝k(1,1,1,…,1)T．对λ2＝1－b,故A的属于λ2的全部特征向量为k2ξ2＋k3ξ3＋…＋knξn,其中ξ2＝(1,－1,0,…,0)T,ξ2＝(1,0,－1,…,0)T,…,ξ2＝(1,0,0,…,－1)T．2°当b＝0时,特征值为λ1＝…＝λn＝1,任意非零列向量均为特征向量．(2)1°当b≠0时,A有n个线性无关的特征向量,令P＝(ξ1,ξ2,…,ξn),则2°当b＝0时,A＝E,对任意可逆矩阵P,均有P－1AP＝E．