设3阶实对称矩阵A的秩为2 λ1＝λ2＝6是A的二重特征值．若α1＝(1 1 0)T α2＝(2 1

大学本科已帮助：人时间:2024-11-15 02:42:42

设3阶实对称矩阵A的秩为2，λ1＝λ2＝6是A的二重特征值．若α1＝(1，1，0)T，α2＝(2，1，1)T，α3＝(－1，2，－3)T，都是A的属于特征值6的特征向量． (1)求A的另一特征值和对应的特征向量； (2)求矩阵A．
请帮忙给出正确答案和分析，谢谢！

456***102

2024-11-15 02:42:42



正确答案：(1)λ＝0k(－111)^Tk≠0．(2)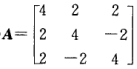
(1)λ＝0,k(－1,1,1)T,k≠0．(2)

讨论f(z)=|z|2的可导性．请帮忙给出正确答案和分析谢谢！

讨论f(z)=|z|2的可导性．请帮忙给出正确答案和分析，谢谢！
设A是n阶实对称矩阵 P是n阶可逆矩阵已知n维列向量α是A的属于特征值A的特征向量则矩阵(P-1

设A是n阶实对称矩阵，P是n阶可逆矩阵，已知n维列向量α是A的属于特征值A的特征向量，则矩阵(P-1AP)T属于特征值A的特征向量是( )．A．P-1αB．PTαC．Pα
基因(gene)请帮忙给出正确答案和分析谢谢！

基因(gene)请帮忙给出正确答案和分析，谢谢！
设A B为n阶矩阵且A与B相似 E为n阶单位矩阵则A．λE－A＝λE－B．B．A与B有相同的特征

设A，B为n阶矩阵，且A与B相似，E为n阶单位矩阵，则A．λE－A＝λE－B．B．A与B有相同的特征值和特征向量．C．A与B都相似于一个对角矩阵．D．对任意常数t
求下列复数的辐角主值： (1)e－1－2i； (2)eiβ－eiβ(0≤β

求下列复数的辐角主值： (1)e－1－2i； (2)eiβ－eiβ(0≤β<α≤2π)．请帮忙给出正确答案和分析，谢谢！

讨论f(z)=|z|2的可导性．请帮忙给出正确答案和分析谢谢！