求齐次线性方程 求非齐次线性方程的实通解:求非齐次线性方程的实通解: 请帮忙给出正确答案和分析 谢谢
求齐次线性方程 求非齐次线性方程的实通解:
求非齐次线性方程的实通解: 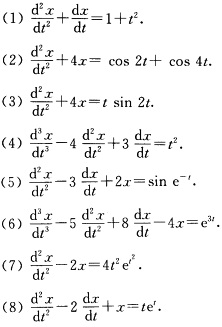
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(1)该方程对应的齐次线性方程的特征多项式为λ2+λ因此特征根为0一1.故原方程对应的齐次线性方程有实基本解组1e-t.又原方程有特解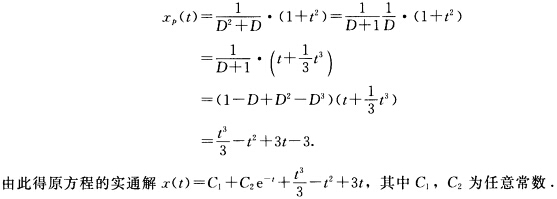 (2)该方程对应的齐次线性方程的特征多项式为λ2+4因此特征根为±2i.故原方程对应的齐次线性方程有实基本解组cos 2tsin 2t.又原方程有特解
(2)该方程对应的齐次线性方程的特征多项式为λ2+4因此特征根为±2i.故原方程对应的齐次线性方程有实基本解组cos 2tsin 2t.又原方程有特解 (3)该方程对应的齐次线性方程的特征多项式为λ2+4因此特征根为+2i.故原方程对应的齐次线性方程有实基本解组cos2tsin 2t.又原方程有特解
(3)该方程对应的齐次线性方程的特征多项式为λ2+4因此特征根为+2i.故原方程对应的齐次线性方程有实基本解组cos2tsin 2t.又原方程有特解 (4)该方程对应的齐次线性方程的特征多项式为λ3-4λ2+3λ因此特征根为0l3故原方程对应的齐次线性方程有实基本解组1ete3t又原方程有特解
(4)该方程对应的齐次线性方程的特征多项式为λ3-4λ2+3λ因此特征根为0l3故原方程对应的齐次线性方程有实基本解组1ete3t又原方程有特解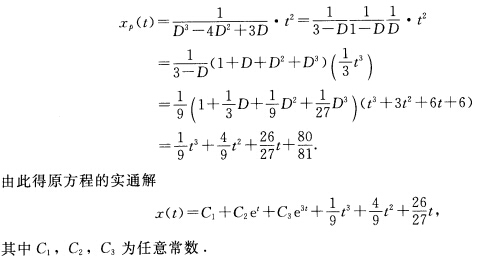 (5)该方程对应的齐次线性方程的特征多项式为λ2-3λ+2因此特征根为12.故原方程对应的齐次线性方程有实基本解组ete2t.又原方程有特解
(5)该方程对应的齐次线性方程的特征多项式为λ2-3λ+2因此特征根为12.故原方程对应的齐次线性方程有实基本解组ete2t.又原方程有特解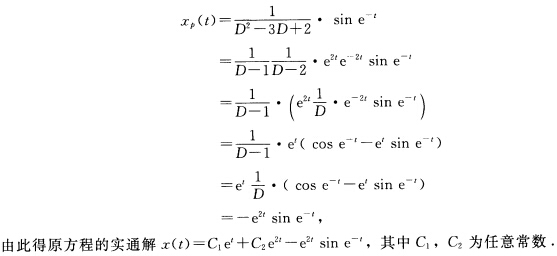 (6)该方程对应的齐次线性方程的特征多项式为λ3一5λ2+8λ一4因此特征根为12(二重根).故原方程对应的齐次线性方程有实基本解组ete2tte2t.又原方程有特解
(6)该方程对应的齐次线性方程的特征多项式为λ3一5λ2+8λ一4因此特征根为12(二重根).故原方程对应的齐次线性方程有实基本解组ete2tte2t.又原方程有特解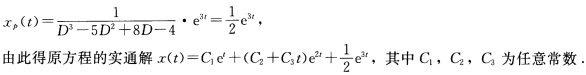 (7)
(7) (8)
(8)
(1)该方程对应的齐次线性方程的特征多项式为λ2+λ,因此特征根为0,一1.故原方程对应的齐次线性方程有实基本解组1,e-t.又原方程有特解(2)该方程对应的齐次线性方程的特征多项式为λ2+4,因此特征根为±2i.故原方程对应的齐次线性方程有实基本解组cos2t,sin2t.又原方程有特解(3)该方程对应的齐次线性方程的特征多项式为λ2+4,因此特征根为+2i.故原方程对应的齐次线性方程有实基本解组cos2t,sin2t.又原方程有特解(4)该方程对应的齐次线性方程的特征多项式为λ3-4λ2+3λ,因此特征根为0,l,3,故原方程对应的齐次线性方程有实基本解组1,et,e3t,又原方程有特解(5)该方程对应的齐次线性方程的特征多项式为λ2-3λ+2,因此特征根为1,2.故原方程对应的齐次线性方程有实基本解组et,e2t.又原方程有特解(6)该方程对应的齐次线性方程的特征多项式为λ3一5λ2+8λ一4,因此特征根为1,2(二重根).故原方程对应的齐次线性方程有实基本解组et,e2t,te2t.又原方程有特解(7)(8)
相似问题
524179386请帮忙给出正确答案和分析 谢谢!
524179386请帮忙给出正确答案和分析,谢谢!
求微分方程 求方程 的奇解(若有的话).求方程 的奇解(若有的话).请帮忙给出正确答案和分析 谢谢
求微分方程 求方程 的奇解(若有的话).求方程 的奇解(若有的话).请帮忙给出正确答案和分析,谢谢!
某厂年计划产量比去年提高8% 实际只提高5% 因此只完成计划的50%。( )此题为判断题(对 错)。
某厂年计划产量比去年提高8%,实际只提高5%,因此只完成计划的50%。( )此题为判断题(对,错)。请帮忙给出正确答案和分析,谢谢!
试求初值问题 考虑初值问题 将区间[一1 1]分为8等份并构造出相应的Euler折线φ(t) 将初值
试求初值问题 考虑初值问题 将区间[一1,1]分为8等份并构造出相应的Euler折线φ(t),将初值问题考虑初值问题 将区间[一1,1]分为8等份并构造出相应
利用Picard逐次逼近法求解初值问题 设x(t)是区间α≤t≤β上的连续函数 且当α≤t≤β时
利用Picard逐次逼近法求解初值问题 设x(t)是区间α≤t≤β上的连续函数,且当α≤t≤β时, 其中L,M是设x(t)是区间α≤t≤β上的连续函数,且当α≤t












