利用Picard逐次逼近法求解初值问题 设x(t)是区间α≤t≤β上的连续函数 且当α≤t≤β时
利用Picard逐次逼近法求解初值问题 设x(t)是区间α≤t≤β上的连续函数,且当α≤t≤β时, 其中L,M是
设x(t)是区间α≤t≤β上的连续函数,且当α≤t≤β时,  其中L,M是非负常数.试用逐次逼近法证明:
其中L,M是非负常数.试用逐次逼近法证明: 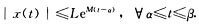
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:不失一般性可设x(t)≥0.由假设可知存在区间[αβ上的连续函数r(t)≤0使得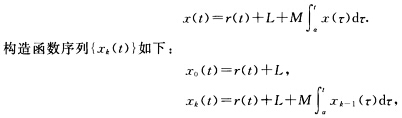 其中k=12….容易归纳地证明对任意自然数k函数xk(t)在[αβ上有定义并且连续.由于x0(t)在[αβ上连续因此存在常数L0>0使得在[αβ上|x0(t)|≤L0 由数学归纳法可证明对任意自然数k
其中k=12….容易归纳地证明对任意自然数k函数xk(t)在[αβ上有定义并且连续.由于x0(t)在[αβ上连续因此存在常数L0>0使得在[αβ上|x0(t)|≤L0 由数学归纳法可证明对任意自然数k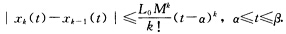 仿照配套教材中定理3.1的证明可知函数序列{xk(t)在区间[αβ上是一致收敛的设
仿照配套教材中定理3.1的证明可知函数序列{xk(t)在区间[αβ上是一致收敛的设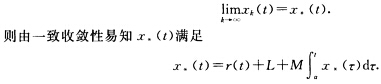 仿照配套教材中定理3.1的证明的第五步可证x(t)≡x*(t).
仿照配套教材中定理3.1的证明的第五步可证x(t)≡x*(t).
不失一般性,可设x(t)≥0.由假设可知存在区间[α,β上的连续函数r(t)≤0使得其中k=1,2,….容易归纳地证明,对任意自然数k,函数xk(t)在[α,β上有定义并且连续.由于x0(t)在[α,β上连续,因此存在常数L0>0使得在[α,β上|x0(t)|≤L0由数学归纳法可证明,对任意自然数k,仿照配套教材中定理3.1的证明可知函数序列{xk(t)在区间[α,β上是一致收敛的,设仿照配套教材中定理3.1的证明的第五步可证x(t)≡x*(t).
相似问题
(99考研题)记为f(x) 则f(x)=0的根的个数为( )A.1B.2C.3D.4请帮忙给出正确答
(99考研题)记为f(x),则f(x)=0的根的个数为( )A.1B.2C.3D.4请帮忙给出正确答案和分析,谢谢!
下列指标中的比例相对指标是( )。A.某厂工人中 技术工人与辅助工人人数之比为4:5B.某年全国高考
下列指标中的比例相对指标是( )。A.某厂工人中,技术工人与辅助工人人数之比为4:5B.某年全国高考录取与报考之比是:1:2C.存款利息率D.家庭收支比E
求微分方程 求解隐式方程求解隐式方程 请帮忙给出正确答案和分析 谢谢!
求微分方程 求解隐式方程求解隐式方程 请帮忙给出正确答案和分析,谢谢!
讨论非线性方程组 的零解稳定性.请帮忙给出正确答案和分析 谢谢!
讨论非线性方程组 的零解稳定性.请帮忙给出正确答案和分析,谢谢!
设n≥2 证明:如果n级矩阵A的元素为1或一1 则|A|必为偶数.请帮忙给出正确答案和分析 谢谢!
设n≥2,证明:如果n级矩阵A的元素为1或一1,则|A|必为偶数.请帮忙给出正确答案和分析,谢谢!












