证明:任意一个秩为r(>0)的矩阵都可以表示成r个秩为1的矩阵之和.请帮忙给出正确答案和分析 谢谢!
证明:任意一个秩为r(>0)的矩阵都可以表示成r个秩为1的矩阵之和.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:设R(A)=r(>0)根据推论4则存在可逆矩阵PQ使得: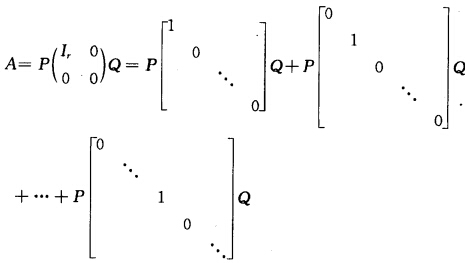 =A1+A2+…+Ar且R(Ai)=1i=12…r.所以A可以表示为r个秩为1的矩阵之和.
=A1+A2+…+Ar且R(Ai)=1i=12…r.所以A可以表示为r个秩为1的矩阵之和.
设R(A)=r(>0)根据推论4则存在可逆矩阵P,Q使得:=A1+A2+…+Ar且R(Ai)=1,i=1,2,…,r.所以A可以表示为r个秩为1的矩阵之和.
相似问题
已知α1=(1 一1 1)T α2=(1 t 一1)T α3=(t 1 2)T β=(4 t 一4)
已知α1=(1,一1,1)T,α2=(1,t,一1)T,α3=(t,1,2)T,β=(4,t,一4)T,若卢可由α1,α2,α3线性表出且表示法不唯一,求t及β的表达式.请帮忙给
如果A是实对称矩阵 并且A是幂零矩阵 则A=0.请帮忙给出正确答案和分析 谢谢!
如果A是实对称矩阵,并且A是幂零矩阵,则A=0.请帮忙给出正确答案和分析,谢谢!
判下列两个矩阵是否相抵:请帮忙给出正确答案和分析 谢谢!
判下列两个矩阵是否相抵:请帮忙给出正确答案和分析,谢谢!
设A是实数域上的n级可逆矩阵 证明:A可以分解成A=TB 其中丁是正交矩阵 B是上三角矩阵 并且B的
设A是实数域上的n级可逆矩阵,证明:A可以分解成A=TB,其中丁是正交矩阵,B是上三角矩阵,并且B的主对角元都为正数;证明这种分解是唯一的.请帮忙给出正
设α=(3 一2 一1 1)T β=(-3 1 一2 1)T.求向量γ=(c1 c2 c3 c4)T
设α=(3,一2,一1,1)T,β=(-3,1,一2,1)T.求向量γ=(c1,c2,c3,c4)T,使2α+3γ=β请帮忙给出正确答案和分析,谢谢!












