设(1)函数f(z)在区域D内解析 f(z)≠常数; (2)C为D内任一条周线 只要问|ez|在闭圆
设(1)函数f(z)在区域D内解析,f(z)≠常数; (2)C为D内任一条周线,只要问|ez|在闭圆|z—z0|≤1上
问|ez|在闭圆|z—z0|≤1上的何处达到最大?并求出最大值.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:由最大模原理对于整函数ez来说只有在边界|z—z0|=1上的点z=1+z0上ez故取到最大模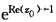 .
.
由最大模原理,对于整函数ez来说,只有在边界|z—z0|=1上的点z=1+z0上ez,故取到最大模.
相似问题
如果在原点解析 而在z=(n=1 2 …)处取下列各组值的函数是否存在:在原点解析 而在z=(n=1
如果在原点解析,而在z=(n=1,2,…)处取下列各组值的函数是否存在:在原点解析,而在z=(n=1,2,…)处取下列各组值的函数是否存在: 请帮忙给出正确答
试判断下列函数的可微性和解析性: (1)f(z)=xy2+ix2y; (2)f(z)=x2+iy2;
试判断下列函数的可微性和解析性: (1)f(z)=xy2+ix2y; (2)f(z)=x2+iy2; (3)f(z)=2x3+3iy3; (4)f(z)=x2一3xy2+i(3x2y—y3).请帮忙给出正确答案和分析,谢谢!
计算下列各复积分: (1)∫C|z|dz 其中C为自原点到1+i的直线段. (2)∫C(z2+sin
计算下列各复积分: (1)∫C|z|dz,其中C为自原点到1+i的直线段. (2)∫C(z2+sin z)dz,其中C为摆线:x=a(θ-sinθ),y=a(1一cosθ)从θ=0到0=2π的
设(1)函数f(z)当|z一z0|>r0>0时是连续的;(2)M(r)表|f(z)|在Kr;|z一z
设(1)函数f(z)当|z一z0|>r0>0时是连续的;(2)M(r)表|f(z)|在Kr;|z一z0|=r>r0上的最大值;(3)=0.试证 请帮忙给出正确答案和分析,谢谢!
判断下列函数的可微性和解析性 若可微并求出其导数. (1)f(z)=(z一1)5; (2)f(z)=
判断下列函数的可微性和解析性,若可微并求出其导数. (1)f(z)=(z一1)5; (2)f(z)=(x2一y2一x)+i(2xy—y2); (3)f(z)=Im z.请帮忙给出正确答案和分析,谢谢!












