计算下列各复积分： (1)∫C｜z｜dz 其中C为自原点到1+i的直线段． (2)∫C(z2+sin
计算下列各复积分： (1)∫C｜z｜dz，其中C为自原点到1+i的直线段． (2)∫C(z2+sin z)dz，其中C为摆线：x=a(θ-sinθ)，y=a(1一cosθ)从θ=0到0=2π的一段． (3)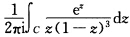
，其中C为不通过0与1的周线．
请帮忙给出正确答案和分析，谢谢！
参考解答
406***103
2024-11-21 14:54:04
正确答案：(1)C的参数方程为：z=t+it0≤t≤1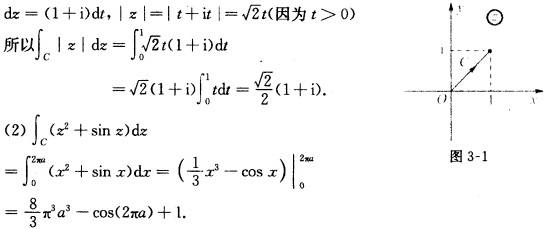
(3)分别就点01与C的各种不同位置关系利用Cauchy积分定理、Cauchy积分公式与高阶求导公式来计算．(I)若点01均不在C内部时如图3—2所示．
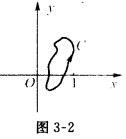则被积函数f(z)=
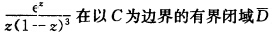上解析由Cauchy积分定理
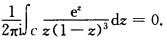(II)若点O在C内部而点1在C外部时如图3—3所示．
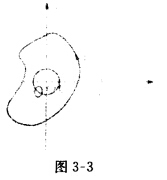则被积函数f(z)=
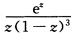在C内部除了奇点z=0外解析以z=0为心ρ为半径作充分小的圆C0：｜z｜=ρ则由复周线C+C0的Cauchy积分定理与Cauchy积分公式知
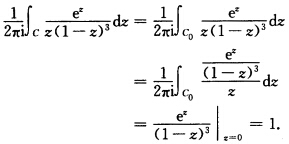(Ⅲ)若z=1在C的内部而点z=0在C的外部如图3—4所示．同理有
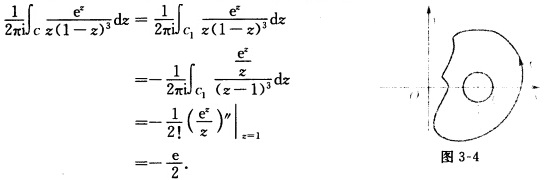(Ⅳ)若z=0与z=1均在C内部如图3—5所示．则由复周线C+C0-+C1-的Cauchy积分定理知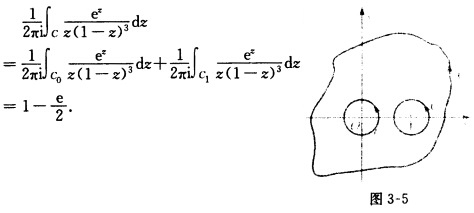
(1)C的参数方程为：z=t+it,0≤t≤1,(3)分别就点0,1与C的各种不同位置关系,利用Cauchy积分定理、Cauchy积分公式与高阶求导公式来计算．(I)若点0,1均不在C内部时,如图3—2所示．则被积函数f(z)=上解析,由Cauchy积分定理(II)若点O在C内部,而点1在C外部时,如图3—3所示．则被积函数f(z)=在C内部除了奇点z=0外解析,以z=0为心,ρ为半径作充分小的圆C0：｜z｜=ρ,则由复周线C+C0的Cauchy积分定理与Cauchy积分公式,知(Ⅲ)若z=1在C的内部,而点z=0在C的外部,如图3—4所示．同理有(Ⅳ)若z=0与z=1均在C内部,如图3—5所示．则由复周线C+C0-+C1-的Cauchy积分定理,知
相似问题
设(1)函数f(z)当｜z一z0｜＞r0＞0时是连续的；(2)M(r)表｜f(z)｜在Kr；｜z一z
设(1)函数f(z)当｜z一z0｜＞r0＞0时是连续的；(2)M(r)表｜f(z)｜在Kr；｜z一z0｜=r＞r0上的最大值；(3)=0．试证 请帮忙给出正确答案和分析，谢谢！
判断下列函数的可微性和解析性 若可微并求出其导数． (1)f(z)=(z一1)5； (2)f(z)=
判断下列函数的可微性和解析性，若可微并求出其导数． (1)f(z)=(z一1)5； (2)f(z)=(x2一y2一x)+i(2xy—y2)； (3)f(z)=Im z．请帮忙给出正确答案和分析，谢谢！
求下列复数的运算． (1)把复数z=一1＋3i表示成指数形式； (2)计算复数解二项方程z4＋a4=
求下列复数的运算． (1)把复数z=一1＋3i表示成指数形式； (2)计算复数解二项方程z4＋a4=0(a＞0)．解二项方程z4+a4=0(a＞0)．请帮忙给出正确答案和分析，谢谢！
试证试证： (1)sin(iz)=isinh z；(2)cos(iz)=cosh z； (3)sin
试证试证： (1)sin(iz)=isinh z；(2)cos(iz)=cosh z； (3)sinh(iz)=isin z： (4)cosh(iz)=cos z； 试证： (1)sin(iz)=isinh z；(2)cos(iz)=cos
计算：(1)∫－2－2＋i (z＋2) 2dz；(2) ∫0π＋2i cos计算(C：｜z｜=2)计
计算：(1)∫－2－2＋i (z＋2) 2dz；(2) ∫0π＋2i cos计算(C：｜z｜=2)计算(C：｜z｜=2) 请帮忙给出正确答案和分析，谢谢！
