判断下列函数的可微性和解析性 若可微并求出其导数． (1)f(z)=(z一1)5； (2)f(z)=

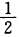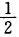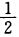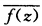正确答案：(1)因为(z一1)在z平面上处处解析由可导函数运算法则知f(z)=(z一1)⁵ 在z平面上处处解析且f'(z)=5(z一1)⁴． (2)因为u(xy)=(x²—y²一x)v(xy)=2xy一y² 所以u_x=2x一1u_y=一2yv_x=2yv_y=2x一2y 此四个偏导数在C上连续又当且仅当y=时C—R方程成立故f(z)仅在直线y=上可导由于直线无平面内点再由解析的定义知f(z)在直线y=上点点不解析从而f(z)在C上处处不解析．所以f(z)=Im z在复平面上处处不可导自然也处处不解析．若函数f(z)在区域D内解析且满足下列条件之一试证f(z)必为常数．(1))在D内解析(2)v=u²．证明不妨设f(z)=u+iv (1)因为f(z)在D内解析所以满足C一R方程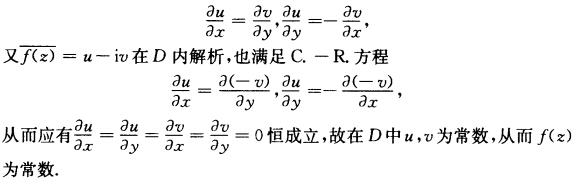(2)因为f(z)在D内解析且有f(z)=u+iu²由C一R方程有故f(z)必为D中常数．
(1)因为(z一1)在z平面上处处解析,由可导函数运算法则,知f(z)=(z一1)5在z平面上处处解析,且f'(z)=5(z一1)4．(2)因为u(x,y)=(x2—y2一x),v(x,y)=2xy一y2,所以ux=2x一1,uy=一2y,vx=2y,vy=2x一2y此四个偏导数在C上连续,又当且仅当y=时,C—R方程成立,故f(z)仅在直线y=上可导,由于直线无平面内点,再由解析的定义知,f(z)在直线y=上点点不解析,从而f(z)在C上处处不解析．所以f(z)=Imz在复平面上处处不可导,自然也处处不解析．若函数f(z)在区域D内解析,且满足下列条件之一,试证f(z)必为常数．(1))在D内解析(2)v=u2．证明不妨设f(z)=u+iv,(1)因为f(z)在D内解析,所以满足C一R方程(2)因为f(z)在D内解析,且有f(z)=u+iu2,由C一R方程,有故f(z)必为D中常数．