设n阶矩阵A的各行元素之和均为零 且R(A)=n-1 求齐次线性方程组Ax=0的通解。请帮忙给出正确
设n阶矩阵A的各行元素之和均为零，且R(A)=n-1，求齐次线性方程组Ax=0的通解。
请帮忙给出正确答案和分析，谢谢！
参考解答
406***101
2024-11-12 23:50:10
正确答案：由于Ax=0的基础解系中所含向量个数为n-R(A)=n-(n-1)-1故Ax=0的任一非零解都可作为它的基础解系。由于n阶矩阵A的各行元素之和均为零因而方程组Ax=0中每一个方程各个未知数的系数之和均为零故ξ=
为Ax=0的一个非零解从而ξ可作为Ax=0的基础解系故得Ax=0的通解为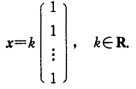
由于Ax=0的基础解系中所含向量个数为n-R(A)=n-(n-1)-1,故Ax=0的任一非零解都可作为它的基础解系。由于n阶矩阵A的各行元素之和均为零,因而方程组Ax=0中每一个方程各个未知数的系数之和均为零,故ξ=为Ax=0的一个非零解,从而ξ可作为Ax=0的基础解系,故得Ax=0的通解为
相似问题
设3阶矩阵A=及3维向量α= 已知Aα与α线性相关 求常数a。请帮忙给出正确答案和分析 谢谢！
设3阶矩阵A=及3维向量α=，已知Aα与α线性相关，求常数a。请帮忙给出正确答案和分析，谢谢！
已知向量组 已知三元非齐次线性方程组Aχ＝β(β≠0) 其增广矩阵的秩r()与系数矩阵A的秩r(A)
已知向量组 已知三元非齐次线性方程组Aχ＝β(β≠0)，其增广矩阵的秩r()与系数矩阵A的秩r(A)都等于2，已知三元非齐次线性方程组Aχ＝β(β≠0)，其增广
二次型的标准形是否唯一?请帮忙给出正确答案和分析 谢谢！
二次型的标准形是否唯一?请帮忙给出正确答案和分析，谢谢！
是否所有的n阶方阵都一定能对角化?请帮忙给出正确答案和分析 谢谢！
是否所有的n阶方阵都一定能对角化?请帮忙给出正确答案和分析，谢谢！
证明向量组a1=构成R3的一个基 并求向量在这个基下的坐标。请帮忙给出正确答案和分析 谢谢！
证明向量组a1=构成R3的一个基，并求向量在这个基下的坐标。请帮忙给出正确答案和分析，谢谢！
