判断下列向量组的线性相关性 并说明理由。 其中α1 α2 α3 α4各不相同。请帮忙给出正确答案
判断下列向量组的线性相关性，并说明理由。 
， 其中α1，α2，α3，α4各不相同。
请帮忙给出正确答案和分析，谢谢！
参考解答
406***101
2024-11-12 20:01:24
正确答案：设有x1x2x3x4使x1α1+x2α2+x3α3+x4α4=0成立则齐次线性方程组的系数行列式为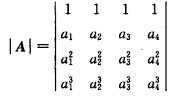
=(α4-α3)(α4-α2)(α4-α1)(α3-α2)(α3-α1)(α2-α1)由于α1α2α3α4各不相同可知|A|≠0则方程组只有唯一零解故向量组α1α2α3α4线性无关。
设有x1,x2,x3,x4,使x1α1+x2α2+x3α3+x4α4=0成立,则齐次线性方程组的系数行列式为=(α4-α3)(α4-α2)(α4-α1)(α3-α2)(α3-α1)(α2-α1),由于α1,α2,α3,α4各不相同,可知|A|≠0,则方程组只有唯一零解,故向量组α1,α2,α3,α4线性无关。
相似问题
举例说明：若两个同阶方阵A与B的特征值分别为λ与μ 则λ＋μ未必为A＋B的特征值。A的行列式|A|
举例说明：若两个同阶方阵A与B的特征值分别为λ与μ，则λ＋μ未必为A＋B的特征值。A的行列式|A|。A的行列式|A|。请帮忙给出正确答案和分析，谢谢！
当n阶行列式D中零元素的个数大于n(n-1)时 是否可以断言此行列式D的值一定等于0?请帮忙给出正确
当n阶行列式D中零元素的个数大于n(n-1)时，是否可以断言此行列式D的值一定等于0?请帮忙给出正确答案和分析，谢谢！
矩阵A的两个互不相同的特征值能否对应于同一个特征向量?请帮忙给出正确答案和分析 谢谢！
矩阵A的两个互不相同的特征值能否对应于同一个特征向量?请帮忙给出正确答案和分析，谢谢！
设A为非奇异矩阵(即|A|≠0) 证明：(A*)-1=(A-1)*。请帮忙给出正确答案和分析 谢谢！
设A为非奇异矩阵(即|A|≠0)，证明：(A*)-1=(A-1)*。请帮忙给出正确答案和分析，谢谢！
已知向量组 已知齐次线性方程组 (1)判别此齐次线性方程组是否存在基础解系； (2)若此齐次线已知齐
已知向量组 已知齐次线性方程组 (1)判别此齐次线性方程组是否存在基础解系； (2)若此齐次线已知齐次线性方程组 (1)判别此齐次线性方程组是否存在基
