已知三次Hermite插值多项式满足：H3(χ0)＝f(χ0) H3(χ1)＝f(χ1) H′3(χ
已知三次Hermite插值多项式满足：H3(χ0)＝f(χ0)，H3(χ1)＝f(χ1)，H′3(χ0)＝f′(χ0)，H′3(χ1)＝f′(χ1)。如果增加一节点χ及条件f(χ2)，f′(χ2)，试从H3(χ)构造五次多项式H5(χ)满足： H5(χi)＝f(χi)，H′5(χi)＝f′(χi) (i＝0，1，2)
请帮忙给出正确答案和分析，谢谢！
参考解答
406***102
2024-11-17 08:22:46
正确答案：由Hermite插值算法知 H2n+1＝H2n-1＋αn(χ)yn＋βn(χ)y′n。 所以H5(χ)＝H3(χ)＋α2(χ)f(χ2)＋β2(χ)f′(χ2) 其中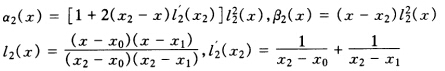
由Hermite插值算法知H2n+1＝H2n-1＋αn(χ)yn＋βn(χ)y′n。所以H5(χ)＝H3(χ)＋α2(χ)f(χ2)＋β2(χ)f′(χ2)其中
相似问题
设二次方程χ2－56χ＋1＝0 若取≈27．98214 并用二次方程求根公式计算两根。 (1)先计算
设二次方程χ2－56χ＋1＝0，若取≈27．98214，并用二次方程求根公式计算两根。 (1)先计算绝对值较大的根χ1，再利用χ1的结果，由韦达定理计算χ2； (
设In∫02χneχ－1dχ (n＝0 1 2…) (1)推证递推算式：In＝1－nIn－1(n＝1
设In∫02χneχ－1dχ (n＝0，1，2…) (1)推证递推算式：In＝1－nIn－1(n＝1，2，3，…)，I0＝1－e－1 (2)若取e－1≈0．36788，试用(1)的递推算式计算
设χj＝χ0＋jh(j＝0 1 2 … n) ωn(χ)＝设χi(j＝0 1 2 … n)为互异节点
设χj＝χ0＋jh(j＝0，1，2，…，n)，ωn(χ)＝设χi(j＝0，1，2，…，n)为互异节点，证明设χi(j＝0，1，2，…，n)为互异节点，证明 请帮忙给出正确答案和分析，谢谢！
设A∈Rn×n为对称正定矩阵 χ∈Rn ‖χ‖＝设矩阵 试求‖A1‖2 ‖A2‖2 ρ(A1) ρ(
设A∈Rn×n为对称正定矩阵，χ∈Rn，‖χ‖＝设矩阵 试求‖A1‖2，‖A2‖2，ρ(A1)，ρ(A2)。设矩阵 试求‖A1‖2，‖A2‖2，ρ(A1)，ρ(A2)。请帮忙给
若TNaOH/HCL＝0．006000g／mL 求此标准溶液的浓度。请帮忙给出正确答案和分析 谢谢！
若TNaOH HCL＝0．006000g／mL，求此标准溶液的浓度。请帮忙给出正确答案和分析，谢谢！
