假设用单纯形方法解线性规划问题 min cx s．t．Ax=b x≥0． 在某次迭代中对应变量xj
假设用单纯形方法解线性规划问题 min cx s．t．Ax=b， x≥0． 在某次迭代中对应变量xj的判别数zj—cj＞0，且单纯形表中相应的列yj=B-1pj≤0．证明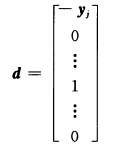 
是可行域的极方向．其中分量1对应xj．
min 3x1一x2 S．t．x1+x2≤9， 0≤xj≤6，j=1，2．
请帮忙给出正确答案和分析，谢谢！
参考解答
4j8***102
2024-11-14 22:01:40
正确答案：×
引进松弛变量x3,写成下列形式：min3x1一x2S．t．x1+x2+x3=9,0≤xi≤6,i=1,2,x3≥0．取初始基本可行解：xB=x3=9,目标函数值f0=0．单纯形表如下：取下界的非基变量下标集R1={1,2,取上界的非基变量下标集[*195,已用符号1标注在表下．选择x2作为进基变量,令x2=0+△2=△2,计算△2：β2=∞,β3=6—0=6,令△2=min{9,∞,6)=6,因此,x2=6,取值上界,仍为非基变量,基变量是x3,取值改变：xB=x3=b—y2△2=9—6=3,f=f0一(z2一c2)x2=0—1×6=一6．修改单纯形表如下：已经达到最优,最优解=(0,6,3),最优值fmin=一6．
相似问题
设S={x|Ax≥b} 其中A是m×n矩阵 m＞n A的秩为n．证明x(0)是S的极点的充要条件是A
设S={x|Ax≥b}，其中A是m×n矩阵，m＞n，A的秩为n．证明x(0)是S的极点的充要条件是A和b可作如下分解： 其中，A1有n个行，且A1的秩为n，b1是n维列向量
问分式线性映射求一个把右半平面映射成单位圆的映射．求一个把右半平面映射成单位圆的映射．请帮忙给出正确
问分式线性映射求一个把右半平面映射成单位圆的映射．求一个把右半平面映射成单位圆的映射．请帮忙给出正确答案和分析，谢谢！
证明设S是Rn中一个非空开凸集 f是定义在S上的可微实函数．如果对任意两点x(1) x(2)∈S 有
证明设S是Rn中一个非空开凸集，f是定义在S上的可微实函数．如果对任意两点x(1)，x(2)∈S，有(x(1)一x(设S是Rn中一个非空开凸集，f是定义在S上的可微实函
问分式线性映射将单位圆盘|z|≤1映为w平面上的什么区域?请帮忙给出正确答案和分析 谢谢！
问分式线性映射将单位圆盘|z|≤1映为w平面上的什么区域?请帮忙给出正确答案和分析，谢谢！
给定下列线性规划问题 max 10x1+7x2+30x3+2x4 s．t． x1 —6x3+x4≤一
给定下列线性规划问题 max 10x1+7x2+30x3+2x4 s．t． x1 —6x3+x4≤一2， x1+x2+5x3一x4≤一7， x2，x3，x4≤0． (1)写出上述原问题的对偶问题．
