证明设S是Rn中一个非空开凸集 f是定义在S上的可微实函数．如果对任意两点x(1) x(2)∈S 有
证明设S是Rn中一个非空开凸集，f是定义在S上的可微实函数．如果对任意两点x(1)，x(2)∈S，有(x(1)一x(
设S是Rn中一个非空开凸集，f是定义在S上的可微实函数．如果对任意两点x(1)，x(2)∈S，有(x(1)一x(2))T
(x(2))≥0蕴含f(x(1))≥f(x(2))，则称f(x)是伪凸函数． 试证明：若f(x)是开凸集S上的伪凸函数，且对某个
，则
是f(x)在S上的全局极小点．
请帮忙给出正确答案和分析，谢谢！
参考解答
420***102
2024-11-14 21:49:31
正确答案：设存在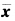
∈S使得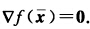
．由于f(x)是开凸集S上的伪凸函数按伪凸函数的定义对任意的x∈S
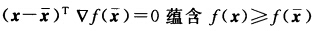因此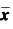
是f(x)在S上的全局极小点．
设存在∈S使得．由于f(x)是开凸集S上的伪凸函数,按伪凸函数的定义,对任意的x∈S,,因此是f(x)在S上的全局极小点．
相似问题
问分式线性映射将单位圆盘|z|≤1映为w平面上的什么区域?请帮忙给出正确答案和分析 谢谢！
问分式线性映射将单位圆盘|z|≤1映为w平面上的什么区域?请帮忙给出正确答案和分析，谢谢！
给定下列线性规划问题 max 10x1+7x2+30x3+2x4 s．t． x1 —6x3+x4≤一
给定下列线性规划问题 max 10x1+7x2+30x3+2x4 s．t． x1 —6x3+x4≤一2， x1+x2+5x3一x4≤一7， x2，x3，x4≤0． (1)写出上述原问题的对偶问题．
求图8．1所示周期函数的拉氏变换． 求下列图8．2所示函数f(t)的拉氏变换．求下列图8．2所示函数
求图8．1所示周期函数的拉氏变换． 求下列图8．2所示函数f(t)的拉氏变换．求下列图8．2所示函数f(t)的拉氏变换． 请帮忙给出正确答案和分析，谢谢！
min 一2x1+x2+x3+10x4 s．t． 一x1+x2+x3+x4=20 2x1一x2+2
min 一2x1+x2+x3+10x4 s．t． 一x1+x2+x3+x4=20， 2x1一x2+2x4=10， xj≥0， j=1，2，3，4．请帮忙给出正确答案和分析，谢谢！
用关于变量有界情形的单纯形方法解下列问题：min －x1一8x2—5x3—6x4 s．t． x1＋4
用关于变量有界情形的单纯形方法解下列问题：min －x1一8x2—5x3—6x4 s．t． x1＋4x2＋5x3＋2x4≤7， min -x1一8x2—5x3—6x4 s．t． x1+4x2+5x3
