设A与B均为n阶方阵 下列说法是否正确?为什么? (1)(A+B)2=A2+2AB+B2； (2)(
设A与B均为n阶方阵，下列说法是否正确?为什么? (1)(A+B)2=A2+2AB+B2； (2)(A+B)(A-B)-A2-B2； (3)(AB)2=A2B2。
此题为判断题(对，错)。请帮忙给出正确答案和分析，谢谢！
参考解答
4j8***101
2024-11-12 23:05:02
正确答案：(1)不正确。因为矩阵乘法不满足交换律。即在一般情况下AB≠BA而(A+B)2=(A+B)(A+B)=A2+AB+BA+B2故(A+B)2≠A2+2AB+B2。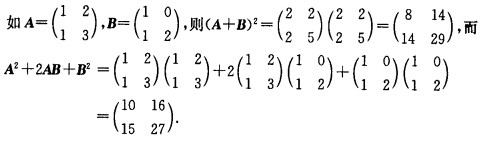
(2)不正确。因为矩阵乘法不满足交换律如
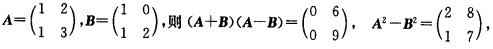故(A+B)(A-B)≠A2-B2。(3)不正确因为矩阵乘法不满足交换律同样取
则(AB)2=
A2B2=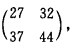
故(AB)2≠A2B2。
相似问题
已知四元非齐次线性方程组Aχ＝β(β≠0) 其增广矩阵若向量组α β γ线性无关 问向量组α α＋β
已知四元非齐次线性方程组Aχ＝β(β≠0)，其增广矩阵若向量组α，β，γ线性无关，问向量组α，α＋β，α＋β＋γ是否若向量组α，β，γ线性无关，问
求下列非齐次线性方程组的通解。 请帮忙给出正确答案和分析 谢谢！
求下列非齐次线性方程组的通解。 请帮忙给出正确答案和分析，谢谢！
设3阶方阵A B满足关系式：A-1BA=6A+BA 其中 求B。请帮忙给出正确答案和分析 谢谢！
设3阶方阵A，B满足关系式：A-1BA=6A+BA，其中 求B。请帮忙给出正确答案和分析，谢谢！
设向量组 若向量组α β γ线性相关 则分量γ＝( )．A．0B．1C．2D．3请帮忙给出正确答案
设向量组 若向量组α，β，γ线性相关，则分量γ＝( )．A．0B．1C．2D．3请帮忙给出正确答案和分析，谢谢！
计算下列四阶行列式 请帮忙给出正确答案和分析 谢谢！
计算下列四阶行列式 请帮忙给出正确答案和分析，谢谢！
