求矩阵A=已知3阶方阵有3个线性无关的特征向量 求x。已知3阶方阵有3个线性无关的特征向量 求x。请
求矩阵A=已知3阶方阵有3个线性无关的特征向量，求x。
已知3阶方阵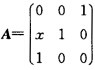
有3个线性无关的特征向量，求x。
请帮忙给出正确答案和分析，谢谢！
参考解答
4j8***101
2024-11-12 20:36:52
正确答案：令|A-λE|=0即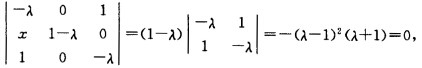
解得特征值分别为λ1=λ2=1λ3=-1。由A有三个线性无关的特征向量知对于λ1=λ2=1A有两个线性无关的特征向量因而R(A-E)=1即A-E=
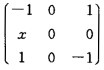的秩为1因此x=0。
令|A-λE|=0,即解得特征值分别为λ1=λ2=1,λ3=-1。由A有三个线性无关的特征向量知,对于λ1=λ2=1,A有两个线性无关的特征向量,因而R(A-E)=1,即A-E=的秩为1,因此x=0。
相似问题
举例说明：若两个同阶方阵A与B的特征值分别为λ与μ 则λ+μ未必为A+B的特征值。A的特征值；请帮忙
举例说明：若两个同阶方阵A与B的特征值分别为λ与μ，则λ+μ未必为A+B的特征值。A的特征值；请帮忙给出正确答案和分析，谢谢！
任何一个矩阵都可以化为阶梯形矩阵 此说法是否正确?为什么?此题为判断题(对 错)。请帮忙给出正确答案
任何一个矩阵都可以化为阶梯形矩阵，此说法是否正确?为什么?此题为判断题(对，错)。请帮忙给出正确答案和分析，谢谢！
设矩阵A=|B－2E|；|B-2E|；请帮忙给出正确答案和分析 谢谢！
设矩阵A=|B－2E|；|B-2E|；请帮忙给出正确答案和分析，谢谢！
设ξ1 ξ2 … ξn-r为n元齐次线性方程组Ax=0的基础解系 而向量组α1 α2 … αn-r是
设ξ1，ξ2，…，ξn-r为n元齐次线性方程组Ax=0的基础解系，而向量组α1，α2，…，αn-r是与基础解系等价的线性无关的向量组，那么向量组α1，α2，…，
设矩阵A为n阶方阵 若A的r阶子式全为零 是否必有|A|=0?请帮忙给出正确答案和分析 谢谢！
设矩阵A为n阶方阵，若A的r阶子式全为零，是否必有|A|=0?请帮忙给出正确答案和分析，谢谢！
