用既约梯度法求解下列问题：min (x1－2)2＋(x2－2)2 s．t． x1＋x2≤2 x1

正确答案：引进松弛变量x₃将(2)题化为 min (x₁-2)²+(x₂—2)² s．t． x₁+x₂+x₃=2 x₁x₂x₃≥0．初始点x⁽¹⁾=(101)^Tf(x⁽¹⁾)=5．目标函数的梯度为▽f(x)=[2(x₁-2)2(x₂一2)0^T． 第1次迭代：x⁽¹⁾=(101)^T ▽f(x⁽¹⁾)=[一2一40^T．令 x_B⁽¹⁾=x₁=1B=[1 ▽_xBf(x)=[一2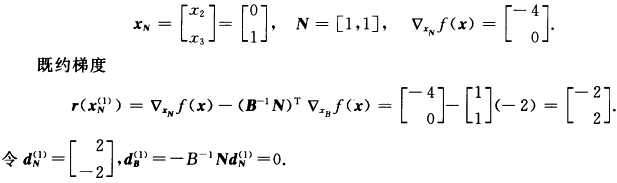 搜索方向d⁽¹⁾=[02一2^T．从x⁽¹⁾出发沿d⁽¹⁾搜索： min f(x⁽¹⁾+λd⁽¹⁾) s．t．0≤λ≤λ_max． (1)其中步长上限问题(1)即 min φ(λ)=f(x⁽¹⁾+λd⁽¹⁾) 第2次迭代： x⁽²⁾=(110)^T ▽f(x⁽²⁾)=[一2一20^T．令 x_B⁽²⁾=x₁=1B=[1 ▽_xBf(x)=一2由于x⁽²⁾=(110)^T中x₃⁽²⁾=0因此令x⁽²⁾是K—T点由于给定问题是凸规划因此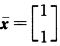是最优解f_min=2．
引进松弛变量x3,将(2)题化为min(x1-2)2+(x2—2)2s．t．x1+x2+x3=2,x1,x2,x3≥0．初始点x(1)=(1,0,1)T,f(x(1))=5．目标函数的梯度为▽f(x)=[2(x1-2),2(x2一2),0T．第1次迭代：x(1)=(1,0,1)T,▽f(x(1))=[一2,一4,0T．令xB(1)=x1=1,B=[1,▽xBf(x)=[一2,搜索方向d(1)=[0,2,一2T．从x(1)出发,沿d(1)搜索：minf(x(1)+λd(1))s．t．0≤λ≤λmax．(1)其中步长上限问题(1)即minφ(λ)=f(x(1)+λd(1))第2次迭代：x(2)=(1,1,0)T,▽f(x(2))=[一2,一2,0T．令xB(2)=x1=1,B=[1,▽xBf(x)=一2,由于x(2)=(1,1,0)T中x3(2)=0,因此令x(2)是K—T点,由于给定问题是凸规划,因此是最优解,fmin=2．