给定函数 f(x)=100(x2一x12)2+(1一x1)2. 求在以下各点处的最速下降方向: 用最
给定函数 f(x)=100(x2一x12)2+(1一x1)2. 求在以下各点处的最速下降方向: 用最速下降法求
用最速下降法求解下列问题: min x12一2x1x2+4x22+x1—3x2. 取初点x(1)=(1,1)T,迭代两次.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:第1次迭代从x(1)出发沿最速下降方向搜索. 设f(x)=x12一2x1x2+4x22+x1—3x2则 取φ(λ)=f(x(1)+λd(1))=(1一λ)2一2(1一λ)(1—3λ)+4(1—3λ)2+(1一λ)一3(1—3λ)令 φ’(λ)=一2(1一λ)+2(1—3λ)+6(1一λ)一24(1—3λ)一1+9=0解得
取φ(λ)=f(x(1)+λd(1))=(1一λ)2一2(1一λ)(1—3λ)+4(1—3λ)2+(1一λ)一3(1—3λ)令 φ’(λ)=一2(1一λ)+2(1—3λ)+6(1一λ)一24(1—3λ)一1+9=0解得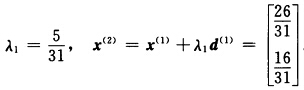 第2次迭代从x(2)出发沿最速下降方向搜索.
第2次迭代从x(2)出发沿最速下降方向搜索.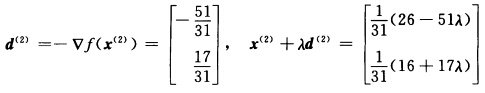 取
取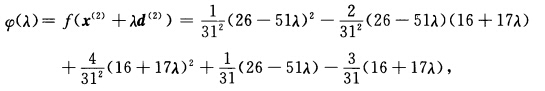 令
令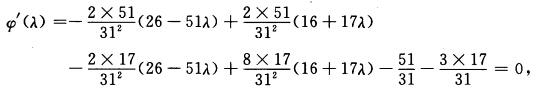 得到
得到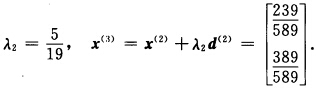
第1次迭代,从x(1)出发沿最速下降方向搜索.设f(x)=x12一2x1x2+4x22+x1—3x2,则取φ(λ)=f(x(1)+λd(1))=(1一λ)2一2(1一λ)(1—3λ)+4(1—3λ)2+(1一λ)一3(1—3λ),令φ’(λ)=一2(1一λ)+2(1—3λ)+6(1一λ)一24(1—3λ)一1+9=0,解得第2次迭代,从x(2)出发,沿最速下降方向搜索.取令得到
相似问题
给定函数 考虑非线性规划问题 min (x1一3)2+(x2—2)2 s.t. x12+x22≤5
给定函数 考虑非线性规划问题 min (x1一3)2+(x2—2)2 s.t. x12+x22≤5, x1+2x2=4, 考虑非线性规划问题 min (x1一3)2+(x2—2)2 s.t.
设将FR共轭梯度法用于有三个变量的函数f(x) 第1次迭代 搜索方向d(1)=(1 一1 2)T 沿
设将FR共轭梯度法用于有三个变量的函数f(x),第1次迭代,搜索方向d(1)=(1,一1,2)T,沿d(1)作精确一维搜索,得到点x(2),又设 那么按共轭梯度法的规
在什么条件下 系统热力学能的改变量和焓变相等 即△U=△H。 判断下列反应的△U与△H是否相等。 (
在什么条件下,系统热力学能的改变量和焓变相等,即△U=△H。 判断下列反应的△U与△H是否相等。 (1)C(s)+O2(g)=CO2(g) (2)N2(g)+3H2(g)=2NH3(g)请帮
给定原问题 min (x1—3)2+(x2—5)2 s.t. 一x12+x2≥0 x1 ≥1 x
给定原问题 min (x1—3)2+(x2—5)2 s.t. 一x12+x2≥0, x1 ≥1, x1+2x2≤10, x1,x2≥0. 写出上述原问题的对偶问题.将原问题中第3个约束
赫斯定律认为化学反应热效应与过程无关 这种说法所以正确是因为反应处在( )。A.可逆条件下进行B.等
赫斯定律认为化学反应热效应与过程无关,这种说法所以正确是因为反应处在( )。A.可逆条件下进行B.等压、无非体积功条件下进行C.等容、不做非体积功条












