用关于变量有界情形的单纯形方法解下列问题：max x1＋2x2＋x3 s．t． x1＋x2＋x3≤1

正确答案：将线性规划记为 maX cx s．t．Ax≤12 x∈S其中x=(x₁x₂x₃)^Tc=(121)A=(111)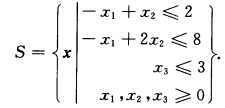 设S有t个极点x^(j)j=12…t有l个极方向d^(j)j=12…l．引入松弛变量v≥0．主规划如下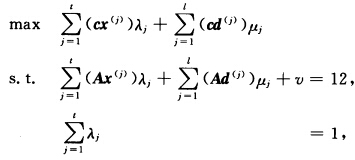：λ_j≥0 j=12…tμ_j≥0 j=12…l v≥0．下面用修正单纯形方法解主规划：取集合S的一个极点x⁽¹⁾=(000)^T初始基变量为v和λ₁初始基B是二阶单位矩阵．单纯形乘子(ωα)=c_BB^-1=(00)约束右端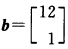现行基本可行解下的目标函数值f=0．初表为 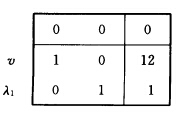第1次迭代： 解子规划求最小判别数： min(ωA一c)x+α s．t．x∈S其中ωA-c=(一1一2一1)上式即 min —x₁一2x₂一x₃ s．t． 一x₁+x₂ ≤2 一x₁+2x₂ ≤8 x₃≤3 x_j≥0 j=123．用单纯形方法求解求得集合S的一个极方向d⁽¹⁾=(210)^T． 主规划中对应μ₁的判别数(ωA一c)d⁽¹⁾=一4μ₁进基主列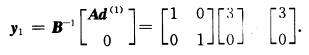用表格形式计算如下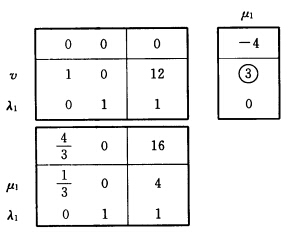：第2次迭代：先解子规划求判别数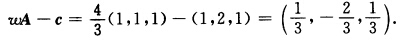：子规划为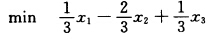 s．t． 一x₁+x₂ ≤2 一x₁+2x₂ ≤8x₃≤3x₁x₂x₃≥0．用单纯形方法求得子规划最优解x⁽²⁾=(460)^T最小值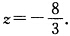λ₂为进基变量主列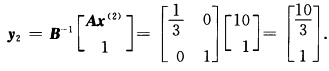用表格形式计算如下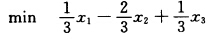：第3次迭代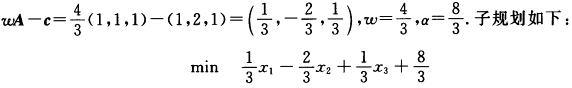：s．t． 一x₁+x₂≤2 一x₁+2x₂≤8 x₃≤3 x₁x₂x₃≥0．子规划最优解x⁽³⁾=(460)^T最优值z=0．结果表明主规划已达最优解．原问题的最优解为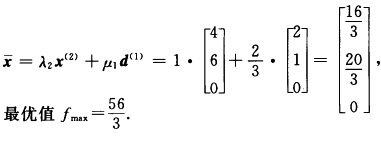
将线性规划记为maXcxs．t．Ax≤12,x∈S,其中x=(x1,x2,x3)T,c=(1,2,1),A=(1,1,1),设S有t个极点x(j),j=1,2,…,t,有l个极方向d(j),j=1,2,…,l．引入松弛变量v≥0．主规划如下：λj≥0,j=1,2,…,t,μj≥0,j=1,2,…,l,v≥0．下面用修正单纯形方法解主规划：取集合S的一个极点x(1)=(0,0,0)T,初始基变量为v和λ1,初始基B是二阶单位矩阵．单纯形乘子(ω,α)=cBB-1=(0,0),约束右端现行基本可行解下的目标函数值f=0．初表为第1次迭代：解子规划,求最小判别数：min(ωA一c)x+αs．t．x∈S,其中ωA-c=(一1,一2,一1),上式即min—x1一2x2一x3s．t．一x1+x2≤2,一x1+2x2≤8,x3≤3,xj≥0,j=1,2,3．用单纯形方法求解,求得集合S的一个极方向,d(1)=(2,1,0)T．主规划中,对应μ1的判别数(ωA一c)d(1)=一4,μ1进基,主列用表格形式计算如下：第2次迭代：先解子规划,求判别数：子规划为s．t．一x1+x2≤2,一x1+2x2≤8,x3≤3,x1,x2,x3≥0．用单纯形方法求得子规划最优解x(2)=(4,6,0)T,最小值λ2为进基变量,主列用表格形式计算如下：第3次迭代：s．t．一x1+x2≤2,一x1+2x2≤8,x3≤3,x1,x2,x3≥0．子规划最优解x(3)=(4,6,0)T,最优值z=0．结果表明,主规划已达最优解．原问题的最优解为