已知f(z)=在z=0的值为1.令z描绘路线OPA(如图2—6)点A为2 试求f(z)在点A的值.
已知f(z)=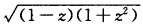 在z=0的值为1.令z描绘路线OPA(如图2—6)点A为2,试求f(z)在点A的值.
在z=0的值为1.令z描绘路线OPA(如图2—6)点A为2,试求f(z)在点A的值. 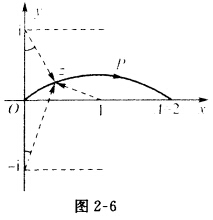
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:f(z)的支点为1±i及∞此时支割线可取为沿虚轴割开[一ii;沿实轴割开[1+∞.路线OPA未穿过支割线记路线OPA为C
f(z)的支点为1,±i及∞,此时支割线可取为,沿虚轴割开[一i,i;沿实轴割开[1,+∞.路线OPA未穿过支割线,记路线OPA为C,
相似问题
设函数f(z)在区域D内解析 且f(z)≠0 试证ln|f(z)|为区域D内的调和函数.请帮忙给出正
设函数f(z)在区域D内解析,且f(z)≠0,试证ln|f(z)|为区域D内的调和函数.请帮忙给出正确答案和分析,谢谢!
试证下列函数在z平面上任何点都不解析: (1)|z|; (2)x+y; (3)Re z; (4).请
试证下列函数在z平面上任何点都不解析: (1)|z|; (2)x+y; (3)Re z; (4).请帮忙给出正确答案和分析,谢谢!
设z=reiθ 试证 Re[ln(z一1)]=试证:在将z平面适当割开后 函数 f(z)= 能分出三
设z=reiθ,试证 Re[ln(z一1)]=试证:在将z平面适当割开后,函数 f(z)= 能分出三个单值解析分支.试证:在将z平面适当割开后,函数 f(z)= 能分出三
试解方程: (1)ez=设=确定在从原点z=0起沿正实轴割破了的z平面上 并且w(i)=一i 试求w
试解方程: (1)ez=设=确定在从原点z=0起沿正实轴割破了的z平面上,并且w(i)=一i,试求w(-i)之值.设=确定在从原点z=0起沿正实轴割破了的z平面上,并且w
判断下列复级数的敛散性 若收敛指明条件收敛还是绝对收敛. 试确定下列幂级数的收敛半径:试确定下列幂级
判断下列复级数的敛散性,若收敛指明条件收敛还是绝对收敛. 试确定下列幂级数的收敛半径:试确定下列幂级数的收敛半径: 请帮忙给出正确答案和分析,谢谢!












