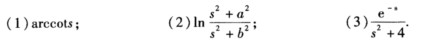参考解答
481***102
2024-11-14 19:57:55
正确答案：反正(余)切函数、对数函数适用微分性质包含指数函数的则适用延迟性质公式为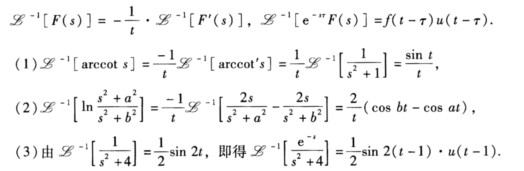 
对于有理函数的拉氏逆变换则先考虑能否进行线性分解或者是把F(s+a)变成F(s)再考虑是否把函数分解成sF(s)或者
最后再考虑像函数的积分性质来求解．
反正(余)切函数、对数函数适用微分性质,包含指数函数的则适用延迟性质,公式为对于有理函数的拉氏逆变换,则先考虑能否进行线性分解或者是把F(s+a)变成F(s),再考虑是否把函数分解成sF(s)或者最后再考虑像函数的积分性质来求解．
相似问题
用定义验证下列各集合是凸集： (1)S={(x1 x2)|x1+2x2≥1 x1—x2≥1)； (2
用定义验证下列各集合是凸集： (1)S={(x1，x2)|x1+2x2≥1，x1—x2≥1)； (2)S={(x1，x2)|x2≥|x1|}； (3)S={(x1，x2)|x12+x22≤10}．请帮忙给出正确答案和分析，谢谢！
证明用单纯形方法求解线性规划问题时 在主元消去前后对应同一变量的判别数有下列关系： 其中(zj一c
证明用单纯形方法求解线性规划问题时，在主元消去前后对应同一变量的判别数有下列关系： 其中(zj一cj)’是主元消去后的判别数，其余是主元消去前的数
求解下列线性规划问题：max 3x1—5x2 s．t． 一x1＋2x2＋4x3≤4 x1＋x2＋2
求解下列线性规划问题：max 3x1—5x2 s．t． 一x1＋2x2＋4x3≤4， x1＋x2＋2x3≤5， 一x1＋2x2max 3x1—5x2 s．t． 一x1+2x2+4x3≤4， x1+x2+2x
求下列幂级数的收敛半径 将函数展开为z的幂级数．将函数展开为z的幂级数．请帮忙给出正确答案和分析 谢
求下列幂级数的收敛半径 将函数展开为z的幂级数．将函数展开为z的幂级数．请帮忙给出正确答案和分析，谢谢！
指出下列函数在零点z=0的级： 若在0＜|z－a|＜R内f(z)解析 (z－a)kf(z)有界 则点
指出下列函数在零点z=0的级： 若在0＜|z－a|＜R内f(z)解析，(z－a)kf(z)有界，则点a是f(z)的不高于若在0＜|z－a|＜R内f(z)解析，(z－a)kf(z)有界，则点a
