应用Euler方法解初值问题 取步长h＝0．1 并与精确解比较。请帮忙给出正确答案和分析 谢谢！
应用Euler方法解初值问题 
取步长h＝0．1，并与精确解比较。
请帮忙给出正确答案和分析，谢谢！
参考解答
481***102
2024-11-17 05:58:41
正确答案：微分方程y′＝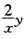
＋χ2eχ 是一阶线性微分方程易解得通解为y＝χ2(eχ＋c) 由y(1)＝0解得c＝－e因此初值问题的解为y＝χ2(eχ－e) 故y(χn)＝χn2(
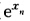－e)(n＝012…) 由显示Euler方法
计算结果如表6．2．1所示。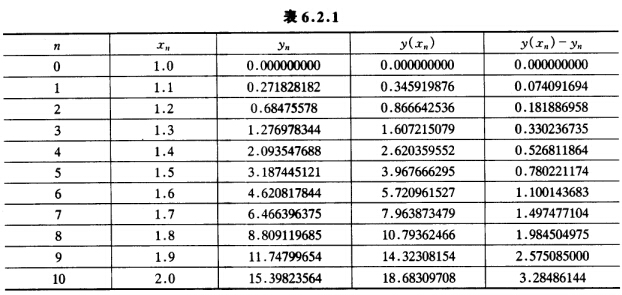
由此可以看出当步长不是很小时Euler方法的精度不高步长取定后n愈大误差愈大。
微分方程y′＝＋χ2eχ是一阶线性微分方程,易解得通解为y＝χ2(eχ＋c)由y(1)＝0解得c＝－e,因此初值问题的解为y＝χ2(eχ－e)故y(χn)＝χn2(－e)(n＝0,1,2,…)由显示Euler方法计算结果如表6．2．1所示。由此可以看出,当步长不是很小时,Euler方法的精度不高,步长取定后,n愈大,误差愈大。
相似问题
已知函数f(χ)＝lnχ和它的导数f′(χ)＝已知函数y＝f(χ)的函数表如下： 试求满足上述函数表
已知函数f(χ)＝lnχ和它的导数f′(χ)＝已知函数y＝f(χ)的函数表如下： 试求满足上述函数表插值已知函数y＝f(χ)的函数表如下： 试求满足上述函数
在1L 0．2500mol·L-1HCl溶液中 需加入( )水 可使HCl溶液对CaO的滴定度TCa
在1L，0．2500mol·L-1HCl溶液中，需加入( )水，可使HCl溶液对CaO的滴定度TCaO HCL＝0．005000g／mL。(MCaO＝56．08)A．201．10mLB．603．2mLC．402．1m
设f(χ)＝sinχ的函数表如下： (1)试分别用线 洼插值以及二次抛物线插值的Lagrange算
设f(χ)＝sinχ的函数表如下： (1)试分别用线，洼插值以及二次抛物线插值的Lagrange算式计算sin 0．3324的值，并估计误差； (2)试用Newton算式的一
称取0．7500g含Na2CO3和K2CO3的试样 溶于水后 加入甲基橙指示剂 滴定至终点 消耗0．
称取0．7500g含Na2CO3和K2CO3的试样，溶于水后，加入甲基橙指示剂，滴定至终点，消耗0．5000mol／L的HCl溶液22．50mL，计算试样中的Na2CO3和K2 CO3的百
设矩阵A的n个特征值互异 对任意的非零向量χ0和y0做迭代 (1)证明：其中 λ1为矩阵A按模最大
设矩阵A的n个特征值互异，对任意的非零向量χ0和y0做迭代 (1)证明：其中，λ1为矩阵A按模最大特征值。 (2)用上述方法求矩阵的按模最大特征值。请帮忙
