判断下列矩阵A=能否对角化若能请求出相似变换矩阵。请帮忙给出正确答案和分析谢谢！

大学本科已帮助：人时间:2024-11-12 20:01:47

判断下列矩阵A=
能否对角化，若能，请求出相似变换矩阵。
请帮忙给出正确答案和分析，谢谢！

473***101

2024-11-12 20:01:47



正确答案：令|A-λE|=0即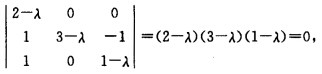则可得A的特征值λ₁=2λ₂=3λ₃=1。对于λ₁=2解(A-2E)x=0由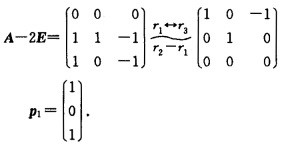可得基础解系
判断3阶方阵是否能够对角化，只需看其是否具有三个线性无关的特征向量。

已知向量组则向量组α1 α2 α3的线性相关性是______．请帮忙给出正确答案和分析谢谢！

已知向量组则向量组α1，α2，α3的线性相关性是______．请帮忙给出正确答案和分析，谢谢！
已知非齐次线性方程组Aχ＝β(β≠0) 若向量η1 η2 都是它的解向量则线性组合2η1＋3η2

已知非齐次线性方程组Aχ＝β(β≠0)，若向量η1，η2，都是它的解向量，则线性组合2η1＋3η2，为非齐次线性方程组( )的解向量．A．Aχ＝β(β≠0)B．A
设矩阵A=请帮忙给出正确答案和分析谢谢！

设矩阵A=请帮忙给出正确答案和分析，谢谢！
判断下列矩阵A=试将下列向量组化为标准正交向量组。试将下列向量组化为标准正交向量组。请帮忙给出正确

判断下列矩阵A=试将下列向量组化为标准正交向量组。试将下列向量组化为标准正交向量组。请帮忙给出正确答案和分析，谢谢！
设A为n阶方阵且令B=A+AT C=A-AT。证明B为对称矩阵 C为反对称矩阵；请帮忙给出正确答案

设A为n阶方阵，且令B=A+AT，C=A-AT。证明B为对称矩阵，C为反对称矩阵；请帮忙给出正确答案和分析，谢谢！

已知向量组则向量组α1 α2 α3的线性相关性是______．请帮忙给出正确答案和分析谢谢！