试求初值问题 证明方程 任一解的存在区间都是有界的.证明方程 任一解的存在区间都是有界的.请帮忙给
试求初值问题 证明方程 任一解的存在区间都是有界的.
证明方程 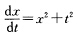 任一解的存在区间都是有界的.
任一解的存在区间都是有界的.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:用反证法.设x=x(t)是初值问题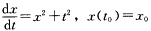 在上式两边从a到t积分得 arctan(x(t))一arctan(x(α))≥t一α.因此对任意t∈[α+∞)均有 t≤α+[arctan(x(t))—arctan(x(α))≤α+π.这显然是不可能的.因此所给方程的任一解向右不能延拓到区间[t0+∞).同样可证它的任一解向左不能延拓到区间(一∞t0.所以它的任一解的存在区间都是有界的.
在上式两边从a到t积分得 arctan(x(t))一arctan(x(α))≥t一α.因此对任意t∈[α+∞)均有 t≤α+[arctan(x(t))—arctan(x(α))≤α+π.这显然是不可能的.因此所给方程的任一解向右不能延拓到区间[t0+∞).同样可证它的任一解向左不能延拓到区间(一∞t0.所以它的任一解的存在区间都是有界的.
用反证法.设x=x(t)是初值问题在上式两边从a到t积分,得arctan(x(t))一arctan(x(α))≥t一α.因此对任意t∈[α,+∞)均有t≤α+[arctan(x(t))—arctan(x(α))≤α+π.这显然是不可能的.因此所给方程的任一解向右不能延拓到区间[t0,+∞).同样可证它的任一解向左不能延拓到区间(一∞,t0.所以它的任一解的存在区间都是有界的.
相似问题
求微分方程 求解高阶方程求解高阶方程 请帮忙给出正确答案和分析 谢谢!
求微分方程 求解高阶方程求解高阶方程 请帮忙给出正确答案和分析,谢谢!
计算下列n阶行列式:请帮忙给出正确答案和分析 谢谢!
计算下列n阶行列式:请帮忙给出正确答案和分析,谢谢!
求微分方程 的通解.请帮忙给出正确答案和分析 谢谢!
求微分方程 的通解.请帮忙给出正确答案和分析,谢谢!
讨论非线性方程组 讨论方程组 是否存在极限环 若有 判定极限环的稳定性.讨论方程组 是否存在极限环
讨论非线性方程组 讨论方程组 是否存在极限环,若有,判定极限环的稳定性.讨论方程组 是否存在极限环,若有,判定极限环的稳定性.请帮忙给出正确
试求初值问题 设函数f(t x)在平面上的条形区域 G={(t x)∈R2:a<t<b |x|<∞}
试求初值问题 设函数f(t,x)在平面上的条形区域 G={(t,x)∈R2:a<t<b,|x|<∞} 上连续且满足不设函数f(t,x)在平面上的条形区域 G={(t,x)∈R2












