利用Picard逐次逼近法求解初值问题 试证明试证明 请帮忙给出正确答案和分析 谢谢！
利用Picard逐次逼近法求解初值问题 试证明
试证明 
请帮忙给出正确答案和分析，谢谢！
参考解答
463***101
2024-11-14 03:40:27
正确答案：用数学归纳法证明．当n=1时显然等式成立．假设当n≤m一1时等式也成立其中m≥2．令n=m设A11(t)=(bij(1))…A1m(t)一(bij(m) )分别为a11(t)…a1m(t)的代数余子式则有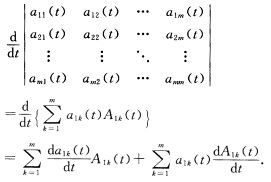
由行列式的性质易见
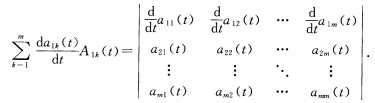再由归纳假设和行列式的性质知
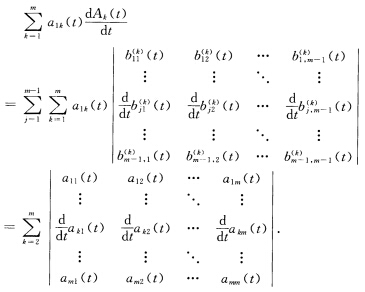因此当n=m时等式也成立． 故所给等式成立．
用数学归纳法证明．当n=1时显然等式成立．假设当n≤m一1时等式也成立,其中m≥2．令n=m,设A11(t)=(bij(1)),…,A1m(t)一(bij(m))分别为a11(t),…,a1m(t)的代数余子式,则有由行列式的性质易见再由归纳假设和行列式的性质知因此当n=m时等式也成立．故所给等式成立．
相似问题
连续变量请帮忙给出正确答案和分析 谢谢！
连续变量请帮忙给出正确答案和分析，谢谢！
试求初值问题 设函数f(t x)在平面上的条形区域G：a＜t＜b ｜x｜＜∞上连续 φ1(t) φ2
试求初值问题 设函数f(t，x)在平面上的条形区域G：a＜t＜b，｜x｜＜∞上连续，φ1(t)，φ2(t)是方程 过同设函数f(t，x)在平面上的条形区域G：a＜t＜b，
求齐次线性方程 求齐次线性方程的实通解：求齐次线性方程的实通解： 请帮忙给出正确答案和分析 谢谢！
求齐次线性方程 求齐次线性方程的实通解：求齐次线性方程的实通解： 请帮忙给出正确答案和分析，谢谢！
求微分方程 已知Riccati方程 有一个特解 求其通解．已知Riccati方程 有一个特解 求其
求微分方程 已知Riccati方程 有一个特解，求其通解．已知Riccati方程 有一个特解，求其通解．请帮忙给出正确答案和分析，谢谢！
车间班组竞赛 结果甲组产量是乙组的2倍 废品总量中甲组占70％ 说明( )。A．甲组产品质量优于乙组
车间班组竞赛，结果甲组产量是乙组的2倍，废品总量中甲组占70％，说明( )。A．甲组产品质量优于乙组B．甲组产品质量不如乙组C．甲组废品率比乙组低D．乙
