求微分方程 已知Riccati方程 有一个特解 求其通解.已知Riccati方程 有一个特解 求其
求微分方程 已知Riccati方程 有一个特解,求其通解.
已知Riccati方程 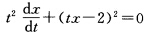 有一个特解
有一个特解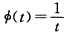 ,求其通解.
,求其通解.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:首先将原方程化为Riccati方程的标准形式 再通过变换y=x一∮(t)将方程(2.37)化为关于y的Bernoulli方程
再通过变换y=x一∮(t)将方程(2.37)化为关于y的Bernoulli方程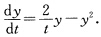 容易求出其通解为
容易求出其通解为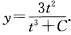 所以原方程的通解为
所以原方程的通解为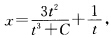 其中C为任意常数。
其中C为任意常数。
首先将原方程化为Riccati方程的标准形式再通过变换y=x一∮(t),将方程(2.37)化为关于y的Bernoulli方程容易求出其通解为所以原方程的通解为其中C为任意常数。
相似问题
车间班组竞赛 结果甲组产量是乙组的2倍 废品总量中甲组占70% 说明( )。A.甲组产品质量优于乙组
车间班组竞赛,结果甲组产量是乙组的2倍,废品总量中甲组占70%,说明( )。A.甲组产品质量优于乙组B.甲组产品质量不如乙组C.甲组废品率比乙组低D.乙
求齐次线性方程 设a b c为正数.试证当t→+∞时 方程 的每一个解都趋于零.设a b c为正数.
求齐次线性方程 设a,b,c为正数.试证当t→+∞时,方程 的每一个解都趋于零.设a,b,c为正数.试证当t→+∞时,方程 的每一个解都趋于零.请帮忙
计算下列2阶行列式:请帮忙给出正确答案和分析 谢谢!
计算下列2阶行列式:请帮忙给出正确答案和分析,谢谢!
证明若xs(t)(s=1 2 … m)分别是方程 不用Liouville公式而直接用变量代换x=x1
证明若xs(t)(s=1,2,…,m)分别是方程 不用Liouville公式而直接用变量代换x=x1(t)y来对方程 降不用Liouville公式而直接用变量代换x=x1(t)y来对方程
(89年考研题)若齐次线性方程组如果n元排列j1j2…jn-1jn的逆序数为r 求排列jnjn-1…
(89年考研题)若齐次线性方程组如果n元排列j1j2…jn-1jn的逆序数为r,求排列jnjn-1…j2j1的逆序数.如果n元排列j1j2…jn-1jn的逆序数为r,求排列jnjn-1












