设n维向量α=(α 0 … 0 α)T α
设n维向量α=(α，0，…，0，α)T，α<0，E为n阶单位矩阵，矩阵A=E一ααT，B=E+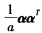
，且B为A的逆矩阵，则α=_____．
请帮忙给出正确答案和分析，谢谢！
参考解答
463***102
2024-11-15 19:13:10
正确答案：一1
∵B=A-1∴AB=E即(E—ααT)(E+ααT)=E—ααT+ααT一α(αα)αγ=E亦即ααT(一1一.2α2)=0由于ααT≠0，故一1一2a=0，再根据a<0可解得a=一1．
相似问题
向量组α1 α2 … αs线性无关的充分条件是( )．A．α1 α2 … αs均不为零向量B．α1
向量组α1，α2，…，αs线性无关的充分条件是( )．A．α1，α2，…，αs均不为零向量B．α1，α2，…，αs中任意两个向量的分量不成比例C．α1，α2，
向量组α1 α2 … αs线性无关的充分条件是A．α1 α2 … αs均不为零向量．B．α1 α2
向量组α1，α2，…，αs线性无关的充分条件是A．α1，α2，…，αs均不为零向量．B．α1，α2，…，αs中任意两个向量的分量不成比例．C．α1，α2，…
如果向量b可以由向量组α1 α2 … α3线性表示 则( )．A．存在一组不全为零的数k21 ．k2
如果向量b可以由向量组α1，α2，…，α3线性表示，则( )．A．存在一组不全为零的数k21，．k2，…，k3使b=k1α1+k2α2+…+k3α3，成立B．存在一组全为零
设有3维列向量 设α1＝(1 1 1) α2＝(1 2 3) α3＝(1 3 t)． (1)问当t为
设有3维列向量 设α1＝(1，1，1)，α2＝(1，2，3)，α3＝(1，3，t)． (1)问当t为何值时，向量组α1，α2，α3线性设α1＝(1，1，1)，α2＝(1，2，3)，
已知A=(a1 a2 a3 a4) 其中a1 a2 a3 a4为四维列向量 方程组AX=0的通解为k
已知A=(a1，a2，a3，a4)，其中a1，a2，a3，a4为四维列向量，方程组AX=0的通解为k(2，一1，1，4)T，则a3可由a1，a2，a4线性表示为_____．请帮忙给出正确答案和分析，谢谢！
