已知β1 β2是非齐次线性方程组Ax=b的两个不同的解 α1 α2是对应齐次线性方程组Ax=0的基础
已知β1、β2是非齐次线性方程组Ax=b的两个不同的解，α1、α2是对应齐次线性方程组Ax=0的基础解系，k1，k2为任意常数，则方程组Ax=b的通解(一般解)必是( )．
A．k1，α1+k2(α1+α2)+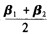
B．k1α1+k2(α1一α2)+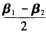
C．k1α1+k2(β1+β2)+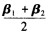
D．k1α1+k2(β1一β2)+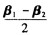
请帮忙给出正确答案和分析，谢谢！
参考解答
463***102
2024-11-15 10:05:04
正确答案：B
本题考查解的性质与解的结构，从a1，a1是Ax=0的基础解系，知Ax=b的通解形式为k1η1+k2η2+ξ，其中，η1，η2是Ax=0的基础解系，ξ是Ax=b的解．由解的性质知：α1，α1+α2α1一α2，β1一β2都是Ax=0的解是Ax=b．那么A中没有特解ξ，C中既没有特解ξ，且β1+β2也不是Ax=0的解．D中虽有特解，但α1，β1一β2的线性相关性不能判定，故A、C、D均不正确．惟B中，是Ax=b的解，α1，α1一α2是Ax=0的线性无关的解，是基础解系．选B．
相似问题
设线性方程组 ① 与方程 x1＋2x2＋x3＝a－1 ② 有公共解 求a的值及所有公共解．请帮忙给出
设线性方程组 ① 与方程 x1＋2x2＋x3＝a－1 ② 有公共解，求a的值及所有公共解．请帮忙给出正确答案和分析，谢谢！
已知线性方程Ax=β的增广矩阵可化为且方程组有无穷多解 则参数A的取值必须满足( )．A．λ=0或λ
已知线性方程Ax=β的增广矩阵可化为且方程组有无穷多解，则参数A的取值必须满足( )．A．λ=0或λ=1B．λ≠0或λ≠1C．λ=0D．λ=1请帮忙给出正确答案和分析，谢谢！
设向量组(Ⅰ)：α1=(α11 α21 α31)T α2=(α12 α22 α32)T α3=(α1
设向量组(Ⅰ)：α1=(α11，α21，α31)T，α2=(α12，α22，α32)T，α3=(α12，α23，α33)T， 向量组(Ⅱ)：β1=(α11，α21，α31,α41)T，β2=(α12
设α1 α2 … αr (r≤n)是互不相同的数 αi=(1 αi αi2 … αin-1)(i=1
设α1，α2，…，αr (r≤n)是互不相同的数，αi=(1，αi，αi2，…，αin-1)(i=1，2，…，r)，问α1，α2，…，αr是否线性相关?请帮忙给出正确答案和分析，谢谢！
设A B为满足AB=O的任意两个非零矩阵 则( )．A．A的列向量组线性相关 B的行向量组线性相关B
设A，B为满足AB=O的任意两个非零矩阵，则( )．A．A的列向量组线性相关，B的行向量组线性相关B．A的列向量组线性相关，B的列向量组线性相关C．A的行向量
