k为何值时 线性方程组 有唯一解 无解 有无穷多组解?在有解的情况下 求出其全部解.请帮忙给出正确答
k为何值时,线性方程组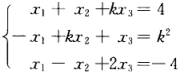 有唯一解、无解、有无穷多组解?在有解的情况下,求出其全部解.
有唯一解、无解、有无穷多组解?在有解的情况下,求出其全部解.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:k≠-1且k≠4有唯一解;k=-1时无解;k=4时有无穷多解.
k≠-1且k≠4有唯一解;k=-1时无解;k=4时有无穷多解.
相似问题
设α1=(2 -1 3 0) α2=(1 2 0 -2) α3=(0 -5 3 4) α4=(-1
设α1=(2,-1,3,0),α2=(1,2,0,-2),α3=(0,-5,3,4),α4=(-1,3,t,0),则________时,α1,α2,α3,α4线性相关.请帮忙给出正确答案和分析,谢谢!
设向量组α1 α2 … αm线性无关 向量β1可用它们线性表示 β2不能用它们线性表示 证明向量组α
设向量组α1,α2,…,αm线性无关,向量β1可用它们线性表示,β2不能用它们线性表示,证明向量组α1,α2,…,αm,λβ1+β2(λ为常数)线性无关.请
k为何值时 线性方程组设线性方程组 (1)证明:若a1 a2 a3 a4两两不相等 则此线性方程组无
k为何值时,线性方程组设线性方程组 (1)证明:若a1,a2,a3,a4两两不相等,则此线性方程组无解; 设线性方程组 (1)证明:若a1,a2,a3,a4两两不相等
设a1 a2 a3 a4是四维非零列向量组 A=(a1 a2 a3 a4) A*为A的伴随矩阵 已知
设a1,a2,a3,a4是四维非零列向量组,A=(a1,a2,a3,a4),A*为A的伴随矩阵,已知方程组AX=0的通解为X=k(0,1,I,0)T,则方程组A*X=0的基础解系为( )
设A是m×n矩阵 Ax=0是非齐次线性方程组Ax=b所对应的齐次线性方程组 则下列结论正确的是A.若
设A是m×n矩阵,Ax=0是非齐次线性方程组Ax=b所对应的齐次线性方程组,则下列结论正确的是A.若Ax=0仅有零解,则Ax=b有唯一解.B.若Ax=0有非零解,












