参考解答
456***101
2024-11-14 04:48:43
正确答案：
直接递推不易得到结果(较低级时可以)变形得Dn一Dn-1=Dn-1—Dn-2=Dn-2一Dn-3=…=D2一D1而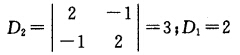
所以Dn一Dn-1=3—2=1于是Dn=Dn-1+1=Dn-2+2=…=D1+(n一1)=2+(n一1)=n+1
直接递推不易得到结果(较低级时可以),变形得Dn一Dn-1=Dn-1—Dn-2=Dn-2一Dn-3=…=D2一D1而所以Dn一Dn-1=3—2=1于是Dn=Dn-1+1=Dn-2+2=…=D1+(n一1)=2+(n一1)=n+1
相似问题
讨论非线性方程组 设α β γ δ ε都是正数 x≥0 y≥0 求出方程组 的所有定常解并讨论其稳定
讨论非线性方程组 设α，β，γ，δ，ε都是正数，x≥0，y≥0，求出方程组 的所有定常解并讨论其稳定性．设α，β，γ，δ，ε都是正数，x≥0，y≥0，
证明若xs(t)(s=1 2 … m)分别是方程 求Airy方程 在t=0处展开的幂级数解．求Air
证明若xs(t)(s=1，2，…，m)分别是方程 求Airy方程 在t=0处展开的幂级数解．求Airy方程 在t=0处展开的幂级数解．请帮忙给出正确答案和分析，谢谢！
证明Cauchy—Euler方程 考虑一个由电感L 电容C和电源E串联组成的简单闭合电路 其中E=E
证明Cauchy—Euler方程 考虑一个由电感L，电容C和电源E串联组成的简单闭合电路，其中E=E0sinωt．试考虑一个由电感L，电容C和电源E串联组成的简单闭合电
讨论非线性方程组 设在xy平面上f(x y)连续可微 给定方程组 证明若在原点的某邻域内有f(x y
讨论非线性方程组 设在xy平面上f(x，y)连续可微，给定方程组 证明若在原点的某邻域内有f(x，y)＞设在xy平面上f(x，y)连续可微，给定方程组 证明若在
证明Cauchy—Euler方程 给定齐次方程组x=Ax 其中A为常数值矩阵．证明 (1)若A的所有
证明Cauchy—Euler方程 给定齐次方程组x=Ax，其中A为常数值矩阵．证明 (1)若A的所有特征根实给定齐次方程组x=Ax，其中A为常数值矩阵．证明 (1)若A的所
