讨论非线性方程组 设在xy平面上f(x y)连续可微 给定方程组 证明若在原点的某邻域内有f(x y
讨论非线性方程组 设在xy平面上f(x，y)连续可微，给定方程组 证明若在原点的某邻域内有f(x，y)＞
设在xy平面上f(x，y)连续可微，给定方程组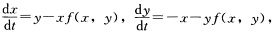 
证明若在原点的某邻域内有f(x，y)＞0，则零解渐近稳定，若有f(x，y)＜0，则零解不稳定．
请帮忙给出正确答案和分析，谢谢！
参考解答
432***101
2024-11-14 04:50:42
正确答案：构造Liapunov函数V(xy)=x2+y2．它是定正的其全导数为
显然当(xy)=(00)时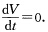
．并且若在原点的某邻域内有f(xy)＞0则在该邻域内
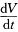为定负函数因此零解渐近稳定；若在原点的某邻域内有f(xy)＜0则在该邻域内
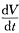为定正函数因此零解不稳定．
构造Liapunov函数V(x,y)=x2+y2．它是定正的,其全导数为显然当(x,y)=(0,0)时,．并且若在原点的某邻域内有f(x,y)＞0,则在该邻域内为定负函数,因此零解渐近稳定；若在原点的某邻域内有f(x,y)＜0,则在该邻域内为定正函数,因此零解不稳定．
相似问题
证明Cauchy—Euler方程 给定齐次方程组x=Ax 其中A为常数值矩阵．证明 (1)若A的所有
证明Cauchy—Euler方程 给定齐次方程组x=Ax，其中A为常数值矩阵．证明 (1)若A的所有特征根实给定齐次方程组x=Ax，其中A为常数值矩阵．证明 (1)若A的所
利用Picard逐次逼近法求解初值问题 在t=0附近求方程 的幂级数解．在t=0附近求方程 的幂级
利用Picard逐次逼近法求解初值问题 在t=0附近求方程 的幂级数解．在t=0附近求方程 的幂级数解．请帮忙给出正确答案和分析，谢谢！
下列属于结构相对指标是( )。A．1998年的积累率为28．5％B．2000年某地区人口密度为114
下列属于结构相对指标是( )。A．1998年的积累率为28．5％B．2000年某地区人口密度为114人／平方公里C．1999年某厂手表产量比上年增长30％D．某单位年成
计算下述n阶行列式：请帮忙给出正确答案和分析 谢谢！
计算下述n阶行列式：请帮忙给出正确答案和分析，谢谢！
利用Picard逐次逼近法求解初值问题 请帮忙给出正确答案和分析 谢谢！
利用Picard逐次逼近法求解初值问题 请帮忙给出正确答案和分析，谢谢！
