计算下列积分计算积分其中C为正向圆周:|z|=4.计算积分其中C为正向圆周:|z|=4.请帮忙给出正
计算下列积分计算积分其中C为正向圆周:|z|=4.
计算积分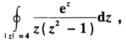 其中C为正向圆周:|z|=4.
其中C为正向圆周:|z|=4.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案: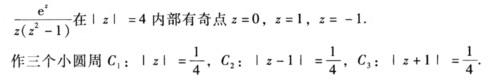 (只要保证三个小圆周互不相交互不包含且均在C内部即可就可利用复合闭路定理)
(只要保证三个小圆周互不相交互不包含且均在C内部即可就可利用复合闭路定理) 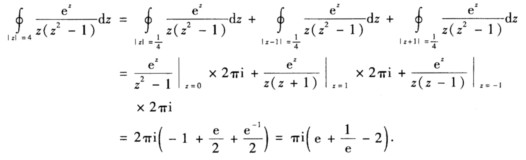
(只要保证三个小圆周互不相交,互不包含且均在C内部即可,就可利用复合闭路定理)
相似问题
下列函数在复平面上何处可导?何处解析? 请帮忙给出正确答案和分析 谢谢!
下列函数在复平面上何处可导?何处解析? 请帮忙给出正确答案和分析,谢谢!
若矩阵A经过有限次初等行变换变为B 则下列结论中错误的是( ).A.A的行向量组与曰的行向量组等价B
若矩阵A经过有限次初等行变换变为B,则下列结论中错误的是( ).A.A的行向量组与曰的行向量组等价B.A的列向量组与刀的列向量组等价C.秩RA=秩RBD.B可
种质(germplasm)请帮忙给出正确答案和分析 谢谢!
种质(germplasm)请帮忙给出正确答案和分析,谢谢!
设λ1 λ2是n阶矩阵A的特征值 α1 α2分别是A的属于λ1 λ2的特征向量 则( ).A.λ1=
设λ1、λ2是n阶矩阵A的特征值,α1、α2分别是A的属于λ1、λ2的特征向量,则( ).A.λ1=λ2时,α1与α2必成比例B.λ1=λ2时,α1与α2必不成比例C
设λ1 λ2是矩阵A的两个特征值 对应的特征向量分别为α1 α1 则( ).A.当λ1=λ2时 α1
设λ1,λ2是矩阵A的两个特征值,对应的特征向量分别为α1,α1,则( ).A.当λ1=λ2时,α1与α2成比例B.当λ1=λ2时,α1与α2不成比例C.当λ1≠λ












