矩阵设四阶方阵A满足条件｜3E＋A｜=0 AAT=2E ｜A｜
矩阵设四阶方阵A满足条件｜3E＋A｜=0，AAT=2E，｜A｜<0．则A的伴随矩阵A*的一个特征值为_____．
设四阶方阵A满足条件｜3E+A｜=0，AAT=2E，｜A｜<0．则A的伴随矩阵A*的一个特征值为_____．
请帮忙给出正确答案和分析，谢谢！
参考解答
432***102
2024-11-15 00:57:23
正确答案：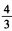
由｜3E+A｜=｜一(一3E—A)｜=0得A的一个特征值为一3．又由｜AAT｜=｜2E｜=24｜E｜=16．因｜A｜<0，故｜A｜=一4．设A的对应于特征值一3的特征向量为α，则Aa=一3a，A-1α=一3-1A-1Aa，即A-1α=一，上式两边同乘｜A｜，则｜A｜A-1α=｜A｜α，即．这样，就得到A*的一个特征值为．
相似问题
下列函数在何处可导?何处解析? (1)f(z)=2x3+3iy3； (2)f(z)=ex(xcos
下列函数在何处可导?何处解析? (1)f(z)=2x3+3iy3； (2)f(z)=ex(xcos y—ysin y)+iex(ycos y+xsin y)； (3)f(z)=xy2+ix2y； (4)f(z)=x2+iy2．请帮忙给出正确答案和分析，谢谢！
计算下列积分设C表示正向圆周求f’(1＋i)．设C表示正向圆周求f’(1+i)．请帮忙给出正确答案和
计算下列积分设C表示正向圆周求f’(1＋i)．设C表示正向圆周求f’(1+i)．请帮忙给出正确答案和分析，谢谢！
设λ0是n阶矩阵A的特征值 且齐次线性方程组(λ0E—A)x=0的基础解系为η1 η2 则A的属于λ
设λ0是n阶矩阵A的特征值，且齐次线性方程组(λ0E—A)x=0的基础解系为η1，η2，则A的属于λ0的全部特征向世为( )．A．η1和η2B．η1，或η2C．c1η1+c
向量组α1=(1 0 2 3) a2=(1 1 3 5) a3=(1 一1 t+2 1) ad=(1
向量组α1=(1，0，2，3)，a2=(1，1，3，5)，a3=(1，一1，t+2，1)，ad=(1，2．4，t+9)线性相关，则t=_____．请帮忙给出正确答案和分析，谢谢！
二次型f(x1 x2 x3)=x12+x22+x32-4x2x3的正惯性指数为( )．A．0B．1C
二次型f(x1，x2，x3)=x12+x22+x32-4x2x3的正惯性指数为( )．A．0B．1C．2D．3请帮忙给出正确答案和分析，谢谢！
