试证方程 z+e-z=a(a＞1) 在Re z＞0内只有一个根 且为实根．请帮忙给出正确答案和分析
试证方程 z+e-z=a(a＞1) 在Re z＞0内只有一个根，且为实根．
请帮忙给出正确答案和分析，谢谢！
参考解答
420***103
2024-11-21 05:21:47
正确答案：若z=x+iy满足z=a—e-z则有 z+iy=a—e-xcosy+ie-xsin y即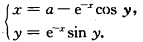
由｜sin y｜≤｜y｜知后一式只可能在y=0时得到满足由此推出原方程只可能有实根． 再从第一式考虑函数x+e-x当x→0时它趋向于1；而当x→+∞时它趋向于+∞．此外(z+e-x)'=1—e-x＞0因此它单调上升因此有且只有一个z满足x+e-x=a这表示在右半平面有且只有一个实根．
若z=x+iy满足z=a—e-z,则有z+iy=a—e-xcosy+ie-xsiny,即由｜siny｜≤｜y｜知,后一式只可能在y=0时得到满足,由此推出,原方程只可能有实根．再从第一式,考虑函数x+e-x,当x→0时,它趋向于1；而当x→+∞时,它趋向于+∞．此外(z+e-x)'=1—e-x＞0,因此它单调上升,因此有且只有一个z满足x+e-x=a,这表示在右半平面有且只有一个实根．
相似问题
若A B相互独立 则下列各式一定成立的是( )．A．B．C．D．请帮忙给出正确答案和分析 谢谢！
若A、B相互独立，则下列各式一定成立的是( )．A．B．C．D．请帮忙给出正确答案和分析，谢谢！
设C是一条围线 其内部D包含点z=0；f(z)与g(z)在D内是解析的 在上连续：g(z)在D内只有
设C是一条围线，其内部D包含点z=0；f(z)与g(z)在D内是解析的，在上连续：g(z)在D内只有一级零点ak，ak≠0(k=1，2，…，n)，求请帮忙给出正确答案和分析，谢谢！
计算积分 如果｜a｜＞ 试证方程 ez=azn(n为正整数) 在圆｜z｜＜R内恰有n个根．如果｜a｜
计算积分 如果｜a｜＞，试证方程 ez=azn(n为正整数) 在圆｜z｜＜R内恰有n个根．如果｜a｜＞，试证方程 ez=azn(n为正整数) 在圆｜z｜＜R内恰有n个根
试证： 设C是一条周线 且设 (1)f(z)符合定理6．9的条件[ak(k=1 2 … p)为f(z
试证： 设C是一条周线，且设 (1)f(z)符合定理6．9的条件[ak(k=1，2，…，p)为f(z)在C内部的不同的设C是一条周线，且设 (1)f(z)符合定理6．9的条件[ak(
考查函数 的奇点类型．请帮忙给出正确答案和分析 谢谢！
考查函数 的奇点类型．请帮忙给出正确答案和分析，谢谢！
