用幂法计算矩阵试用Jacobi方法解矩阵的全部特征值和特征向量。试用Jacobi方法解矩阵的全部特征
用幂法计算矩阵试用Jacobi方法解矩阵的全部特征值和特征向量。
试用Jacobi方法解矩阵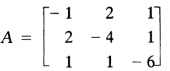 的全部特征值和特征向量。
的全部特征值和特征向量。
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:×
令A0=A,|aij(0)|=|a12(0)|=2,故取cot2θ=得c=cosθ=0.8944271910,s=sinθ=0.4472135955,则如此继续,可得将计算中|aij|<×10-8的元素近似为零,则最后得故得A的特征值λ1=0.2879921390,λ2=-4.866925525,λ3=-6.421066615对应的特征向量χ1=(0.8664321533,0.4530577271,0.2098428459)Tχ2=(-0.4974252005,0.8195890122,0.2843273135)Tχ3=(-0.04316820421,-0.3507314461,0.9354806036)T
相似问题
推证等式 试根据nsin(n=3 6 12 24)的值 利用外推法计算π的近似值。请帮忙给出正确答
推证等式 试根据nsin(n=3,6,12,24)的值,利用外推法计算π的近似值。请帮忙给出正确答案和分析,谢谢!
定量分析_________误差影响测定结果的准确度 _____________误差影响测定结果的精密
定量分析_________误差影响测定结果的准确度,_____________误差影响测定结果的精密度。请帮忙给出正确答案和分析,谢谢!
求二次方程aχ2+bχ+c=0根的公式通常形式为χ1= χ2=请帮忙给出正确答案和分析 谢谢!
求二次方程aχ2+bχ+c=0根的公式通常形式为χ1=,χ2=请帮忙给出正确答案和分析,谢谢!
证明方程f(χ)χ3-2χ-3=0在区间[1 2]内有唯一实根。能否断定对任意初值χ0∈(1 2)
证明方程f(χ)χ3-2χ-3=0在区间[1,2]内有唯一实根。能否断定对任意初值χ0∈(1,2),Newton迭代法收敛于实根?若将区间[1,2]改为[,2],Newton法是
设f(χ)=sinχ的函数表如下: 为求代数方程f(χ)=χ4-3x-1=0的根 列出如下的函数表:
设f(χ)=sinχ的函数表如下: 为求代数方程f(χ)=χ4-3x-1=0的根,列出如下的函数表: 试用插值为求代数方程f(χ)=χ4-3x-1=0的根,列出如下












