求nx1+(n-1)x2+…+2xx-1+xn=0的基础解系。请帮忙给出正确答案和分析 谢谢!
求nx1+(n-1)x2+…+2xx-1+xn=0的基础解系。
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:显然R(A)=1故基础解系中含解向量的个数为n-R(A)=n-1个由已知得xn=-nx1-(n-1)x2一…一2xn-1故方程的一般解为 x1x2…xn-1为自由未知量。写成向量形式
x1x2…xn-1为自由未知量。写成向量形式 记x1=k1x2=k2…xn-1=kn-1则方程的通解为
记x1=k1x2=k2…xn-1=kn-1则方程的通解为 且基础解系为
且基础解系为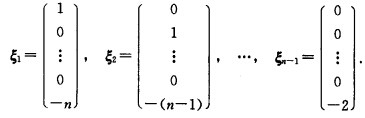
显然R(A)=1,故基础解系中含解向量的个数为n-R(A)=n-1个,由已知得xn=-nx1-(n-1)x2一…一2xn-1,故方程的一般解为x1,x2,…,xn-1为自由未知量。写成向量形式记x1=k1,x2=k2,…,xn-1=kn-1,则方程的通解为且基础解系为
相似问题
求矩阵A=用配方法化二次型f(x1 x2 x3)=x12+5x32+2x1x2+4x2x3为标准形。
求矩阵A=用配方法化二次型f(x1,x2,x3)=x12+5x32+2x1x2+4x2x3为标准形。用配方法化二次型f(x1,x2,x3)=x12+5x32+2x1x2+4x2x3为标准形。请帮忙给出正确答案和分析,谢谢!
判断下列矩阵A=设 求ρ(A)=2A5+3E。设 求ρ(A)=2A5+3E。请帮忙给出正确答案和分析
判断下列矩阵A=设,求ρ(A)=2A5+3E。设,求ρ(A)=2A5+3E。请帮忙给出正确答案和分析,谢谢!
当( )时 向量组α1 α2线性无关.A.向量α1 或α2为零向量B.向量α1且口α2为非零向量C.
当( )时,向量组α1,α2线性无关.A.向量α1,或α2为零向量B.向量α1且口α2为非零向量C.向量α1与α2对应分量成比例D.向量α1与α2对应分量不成
请介绍一下行列式中余子式与代数余子式有何特点?有何联系?请帮忙给出正确答案和分析 谢谢!
请介绍一下行列式中余子式与代数余子式有何特点?有何联系?请帮忙给出正确答案和分析,谢谢!
设P(A)>0 P(A|B)=1 则必有( ).A.P(A∪B)>P(A)B.P(A∪B)>P(B)
设P(A)>0,P(A|B)=1,则必有( ).A.P(A∪B)>P(A)B.P(A∪B)>P(B)C.P(A∪B)=P(A)D.P(A∪B)=P(B)请帮忙给出正确答案和分析,谢谢!












