已知平面简谐波波源在原点处 其波函数为y=Acos(Bt-Cx) 式中A B和C为正值恒量。（1）求
已知平面简谐波波源在原点处，其波函数为y=Acos(Bt-Cx)，式中A、B和C为正值恒量。（1）求振幅、波速、频率和波长；（2）写出波射线上距原点为l处一点的振动方程；（3）求波射线上相距为d的两点间的相差。
请帮忙给出正确答案和分析，谢谢！
参考解答
413***100
2024-11-03 22:21:06
正确答案：（1）已知波函数y=Acos(Bt-Cx) （1）将式（1）变形得到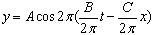
（2）已知平面简谐波波函数的标准形式为y=Acos[2π(vt-
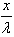)+ψ0 （3）将式（2）与式（3）比较可得A=A 
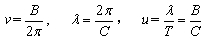（2）将x=l代入已知波动方程式（1）则得到l处质点的振动方程为y=Acos(Bt-Cl) （3）设波射线上任意一点距原点的距离为x另一点距原点的距离为x+d这两点间的相差为△ψ=[Bt-Cx-[Bt-C(x+d)=Cd
（1）已知波函数y=Acos(Bt-Cx)（1）将式（1）变形,得到（2）已知平面简谐波波函数的标准形式为y=Acos[2π(vt-)+ψ0（3）将式（2）与式（3）比较可得A=A,（2）将x=l代入已知波动方程式（1）,则得到l处质点的振动方程为y=Acos(Bt-Cl)（3）设波射线上任意一点距原点的距离为x,另一点距原点的距离为x+d,这两点间的相差为△ψ=[Bt-Cx-[Bt-C(x+d)=Cd
相似问题
初转速为4000 r.min-1的飞轮制动后在6 min内停止。试求：（1）飞轮的平均角加速度；（2
初转速为4000 r min-1的飞轮制动后在6 min内停止。试求：（1）飞轮的平均角加速度；（2）飞轮在制动过程中转过的圈数。请帮忙给出正确答案和分析，谢谢！
半径为R具有光滑轴的定滑轮边缘绕一根轻质细绳 绳的下端挂一个质量为m的物体．绳与定滑轮之间无相对滑动
半径为R具有光滑轴的定滑轮边缘绕一根轻质细绳，绳的下端挂一个质量为m的物体．绳与定滑轮之间无相对滑动．若物体下落的加速度为a，则定滑轮对轴的转动惯
求质量均匀分布的半球体的质心位置。请帮忙给出正确答案和分析 谢谢！
求质量均匀分布的半球体的质心位置。请帮忙给出正确答案和分析，谢谢！
如图4-3所示 劲度系数为k的弹簧一端固定于墙上 另一端与质量为m1的木块相连．木块m1与质量为m2
如图4-3所示，劲度系数为k的弹簧一端固定于墙上，另一端与质量为m1的木块相连．木块m1与质量为m2的木块用轻绳相连．整个系统置于光滑水平面上，然后以恒
距反射壁L处有一个波源 向着反射壁发出角频率为ω 振幅为A的平面波。波的传播速度为u。若选择波源处为
距反射壁L处有一个波源，向着反射壁发出角频率为ω、振幅为A的平面波。波的传播速度为u。若选择波源处为坐标原点O、波传播方向为正方向，初相为零，如图7
