试证下面的定理: 设f(z)=u(r θ)+iv(r θ) z=reiθ 若u(r θ) v(r
试证下面的定理: 设f(z)=u(r,θ)+iv(r,θ),z=reiθ, 若u(r,θ),v(r,θ)在点(r,θ)是可微的,且满足极坐标的C.一R方程: 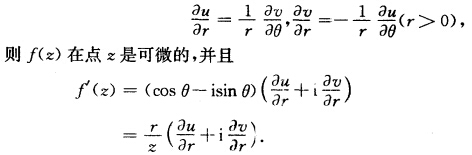 注:这里要适当割破z平面(如沿负实轴割破),否则θ(z)就不是单值的.
注:这里要适当割破z平面(如沿负实轴割破),否则θ(z)就不是单值的.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:由题设条件可知:(1)二元函数u(xy)v(xy)在点(xy)可微;(2)u(xy)v(xy)在点(xy)满足C.一R方程:ux=vyuy=vx 故由数学分析中的反函数存在定理知在相应点(xy)附近函数组①存在唯一具有一阶连续偏导的反函数组
故由数学分析中的反函数存在定理知在相应点(xy)附近函数组①存在唯一具有一阶连续偏导的反函数组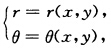 所以r(xy)θ(xy)在点(xy)可微.又因u(rθ)v(rθ)在点(rθ)可微故复合函数u(xy)v(xy)在点(xy)可微.由复合函数反函数求偏导法则及极坐标的C—R方程知
所以r(xy)θ(xy)在点(xy)可微.又因u(rθ)v(rθ)在点(rθ)可微故复合函数u(xy)v(xy)在点(xy)可微.由复合函数反函数求偏导法则及极坐标的C—R方程知 即满足定理2.2的两个条件所以f(z)在点z=z+iy可微.运用复合函数反函数求偏导法则及极坐标C.一R方程得
即满足定理2.2的两个条件所以f(z)在点z=z+iy可微.运用复合函数反函数求偏导法则及极坐标C.一R方程得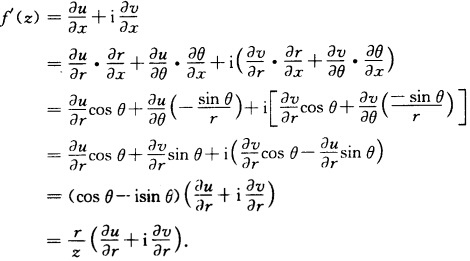
由题设条件可知:(1)二元函数u(x,y),v(x,y)在点(x,y)可微;(2)u(x,y),v(x,y)在点(x,y)满足C.一R方程:ux=vy,uy=vx故由数学分析中的反函数存在定理知,在相应点(x,y)附近,函数组①存在唯一具有一阶连续偏导的反函数组所以,r(x,y),θ(x,y)在点(x,y)可微.又因u(r,θ),v(r,θ)在点(r,θ)可微,故复合函数u(x,y),v(x,y)在点(x,y)可微.由复合函数,反函数求偏导法则及极坐标的C—R方程知即满足定理2.2的两个条件,所以f(z)在点z=z+iy可微.运用复合函数反函数求偏导法则及极坐标C.一R方程,得
相似问题
设函数f(z)当|z—z0|>r0(0<r0<r)时解析 =A 则对任何r>r0 有f(z)dz=A
设函数f(z)当|z—z0|>r0(0<r0<r)时解析,=A,则对任何r>r0,有f(z)dz=A,其中,Kr:|z—z0|=r.请帮忙给出正确答案和分析,谢谢!
设z=x+iy 试证函数 除原点外在全复平面解析 当z≠0时 求出f(z).请帮忙给出正确答案和分
设z=x+iy,试证函数 除原点外在全复平面解析,当z≠0时,求出f(z).请帮忙给出正确答案和分析,谢谢!
试证设a b为复常数 b≠0 试证 cos a+cos(a+b)+…+cos(a+nb) 注:分别证
试证设a、b为复常数,b≠0,试证 cos a+cos(a+b)+…+cos(a+nb) 注:分别证明(1)和(2).由于a设a、b为复常数,b≠0,试证 cos a+cos(a+b)+…+co
已知f(z)=在z=0的值为1.令z描绘路线OPA(如图2—6)点A为2 试求f(z)在点A的值.
已知f(z)=在z=0的值为1.令z描绘路线OPA(如图2—6)点A为2,试求f(z)在点A的值. 请帮忙给出正确答案和分析,谢谢!
设函数f(z)在区域D内解析 且f(z)≠0 试证ln|f(z)|为区域D内的调和函数.请帮忙给出正
设函数f(z)在区域D内解析,且f(z)≠0,试证ln|f(z)|为区域D内的调和函数.请帮忙给出正确答案和分析,谢谢!












