如果设(1)f(z)在区域D内解析; (2)在某一点z0∈D有 f(n)(z0)=0 n=1 2 …
如果设(1)f(z)在区域D内解析; (2)在某一点z0∈D有 f(n)(z0)=0,n=1,2,… 试证f(z)在D内必为
设(1)f(z)在区域D内解析; (2)在某一点z0∈D有 f(n)(z0)=0,n=1,2,… 试证f(z)在D内必为常数.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:因为f(z)在点z0解析由泰勒定理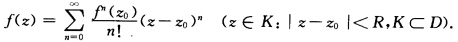 再由题设 f(n)(z0)=0n=12…则f(z)=f(z0)(z∈K
再由题设 f(n)(z0)=0n=12…则f(z)=f(z0)(z∈K D)由唯一性定理得 f(z)≡f(z0)(z∈D).
D)由唯一性定理得 f(z)≡f(z0)(z∈D).
因为f(z)在点z0解析,由泰勒定理再由题设f(n)(z0)=0,n=1,2,…则f(z)=f(z0),(z∈KD)由唯一性定理得f(z)≡f(z0),(z∈D).
相似问题
设f(z)为非常数的整函数 又设R M为任意正数.试证:满足|z|>R且|f(z)|>M的z必存在.
设f(z)为非常数的整函数,又设R,M为任意正数.试证:满足|z|>R且|f(z)|>M的z必存在.请帮忙给出正确答案和分析,谢谢!
试解方程: (1)ez=设w=确定在从原点z=0起沿负实轴割破了的z平面上 并且w(一2)=一(这是
试解方程: (1)ez=设w=确定在从原点z=0起沿负实轴割破了的z平面上,并且w(一2)=一(这是边界上岸点设w=确定在从原点z=0起沿负实轴割破了的z平面上,并且w
试证若z=z+iy 试证: (1)sin z=sin x.cosh y+icos x.sinh y;
试证若z=z+iy,试证: (1)sin z=sin x.cosh y+icos x.sinh y; (2)cos z=cos x.cosh y—isin x.sin若z=z+iy,试证: (1)sin z=sin x
试证多值函数f(z)=在割去线段[一1 1]的z平面上可以分出四个单值解析分支.求函数在割线上岸取正
试证多值函数f(z)=在割去线段[一1,1]的z平面上可以分出四个单值解析分支.求函数在割线上岸取正值的那个分支在点z=±i的值.请帮忙给出正确答案和分析,谢谢!
设(1)函数f(z)在区域D内解析 f(z)≠常数; (2)C为D内任一条周线 只要讨论下列级数的敛
设(1)函数f(z)在区域D内解析,f(z)≠常数; (2)C为D内任一条周线,只要讨论下列级数的敛散性:讨论下列级数的敛散性: 请帮忙给出正确答案和分析,谢谢!












