设有行列式D= 又已知1703 3159 975 10959能被13整除 不计算行列式D 证明D能被
设有行列式D=
，又已知1703，3159，975，10959能被13整除，不计算行列式D，证明D能被13整除。
请帮忙给出正确答案和分析，谢谢！
参考解答
413***101
2024-11-13 00:13:53
正确答案：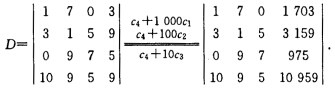
又第四列元素1703315997510959均能被13整除故第四列元素含有公因子13。故行列式能被13整除。
根据行列式D的各行元素的特征，在D中构造出元素1703，3159，975，10959。
相似问题
将多项式f(x)=用ax2+bc+c形式表示出来。请帮忙给出正确答案和分析 谢谢！
将多项式f(x)=用ax2+bc+c形式表示出来。请帮忙给出正确答案和分析，谢谢！
已知四元齐次线性方程组Aχ＝0 若系数矩阵A的秩r(A)＝1 则其基础解系含( )个线性无关解向量．
已知四元齐次线性方程组Aχ＝0，若系数矩阵A的秩r(A)＝1，则其基础解系含( )个线性无关解向量．A．1B．2C．3D．4请帮忙给出正确答案和分析，谢谢！
已知向量组 已知齐次线性方程组 (1)判别此齐次线性方程组是否存在基础解系； (2)若已知齐次线性方
已知向量组 已知齐次线性方程组 (1)判别此齐次线性方程组是否存在基础解系； (2)若已知齐次线性方程组 (1)判别此齐次线性方程组是否存在基础解系；
设B为3阶非零矩阵 且B的每一列均为方程组的解 求λ值和|B|。 请帮忙给出正确答案和分析 谢谢！
设B为3阶非零矩阵，且B的每一列均为方程组的解，求λ值和|B|。 请帮忙给出正确答案和分析，谢谢！
将二次曲面x2+3y2+3z2+2y2-1化为标准形 并指出曲面类型。请帮忙给出正确答案和分析 谢谢
将二次曲面x2+3y2+3z2+2y2-1化为标准形，并指出曲面类型。请帮忙给出正确答案和分析，谢谢！
