将二次曲面x2+3y2+3z2+2y2-1化为标准形 并指出曲面类型。请帮忙给出正确答案和分析 谢谢

正确答案：设(xyz)=x²+3y²+3z²+2yz易知f的矩阵为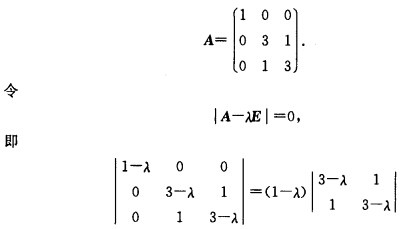=(1-λ)(2-λ)(4-λ)=0则可得A的特征值为λ₁=1λ₂=2λ₃=4。当λ₁=1时解齐次线性方程组(A-E)x=0可得特征向量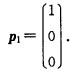当λ₂=2时解齐次线性方程组(A-2E)x=0可得特征向量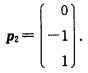当λ₃=4时解齐次线性方程组(A-4E)x=0可得特征向量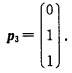对于实对称矩阵不同特征值对应的特征向量已正交故只需对其进行单位化有x'²+2y'²+4z'²=1由此可以判断该曲面为椭球面。
设(x,y,z)=x2+3y2+3z2+2yz,易知f的矩阵为=(1-λ)(2-λ)(4-λ)=0,则可得A的特征值为λ1=1,λ2=2,λ3=4。当λ1=1时,解齐次线性方程组(A-E)x=0,可得特征向量当λ2=2时,解齐次线性方程组(A-2E)x=0,可得特征向量当λ3=4时,解齐次线性方程组(A-4E)x=0,可得特征向量对于实对称矩阵,不同特征值对应的特征向量已正交,故只需对其进行单位化,有x'2+2y'2+4z'2=1,由此可以判断该曲面为椭球面。