问分式线性映射求把上半平面映射成单位圆的分式线性映射w=(z) 并满足条件f(i)=0 f(-1)=
问分式线性映射求把上半平面映射成单位圆的分式线性映射w=(z),并满足条件f(i)=0,f(-1)=1.
求把上半平面映射成单位圆的分式线性映射w=(z),并满足条件f(i)=0,f(-1)=1.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:把上半平面映射成单位圆的分式线性映射w=f(z)的一般形式为 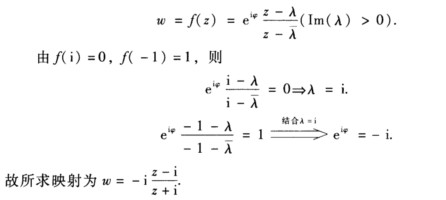
把上半平面映射成单位圆的分式线性映射w=f(z)的一般形式为
相似问题
问分式线性映射把点z=1 i -i分别映射成点w=1 0 -1的分式线性映射把单位圆|z|<1映射成
问分式线性映射把点z=1,i,-i分别映射成点w=1,0,-1的分式线性映射把单位圆|z|<1映射成什么?并求出把点z=1,i,-i分别映射成点w=1,0,-1的分式线
max —x1—3x2—7x3—4x4—6x5 s.t. 一5x1+2x2+6x3一x4+x5一x6
max —x1—3x2—7x3—4x4—6x5 s.t. 一5x1+2x2+6x3一x4+x5一x6 =6, 2x1+x2+x3+x4+2x5 -x7=3, xj≥0,j=1,2,…,7.请帮忙给出正确答案和分析,谢谢!
考虑线性规划问题 min cx s.t. Ax=b x≥0 其中A是m阶对称矩阵 cT=b.证明
考虑线性规划问题 min cx s.t. Ax=b, x≥0, 其中A是m阶对称矩阵,cT=b.证明若x(0)是上述问题的可行解,则它也是最优解.请帮忙给出正确答案和分析,谢谢!
求图8.1所示周期函数的拉氏变换. 求下列卷积: (1)1*1; (2)t*t; (3)tm*tn;
求图8.1所示周期函数的拉氏变换. 求下列卷积: (1)1*1; (2)t*t; (3)tm*tn; 求下列卷积: (1)1*1; (2)t*t; (3)tm*tn; (4)sint*cost.请帮忙给出正确答案和分析,谢谢!
证明设f是Rn上的凸函数 证明:如果f在某点X ∈Rn处具有全局极大值 则对一切点X ∈Rn f(x
证明设f是Rn上的凸函数,证明:如果f在某点X ∈Rn处具有全局极大值,则对一切点X ∈Rn,f(x)为常数.设f是Rn上的凸函数,证明:如果f在某点X ∈Rn处具












