用Gauss顺序消元法解方程组并求系数矩阵的行列式的值。 用Gauss—Jordan消去法解方程组用
用Gauss顺序消元法解方程组并求系数矩阵的行列式的值。 用Gauss—Jordan消去法解方程组
用Gauss—Jordan消去法解方程组 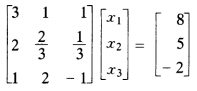
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:对方程组的增广矩阵[Ab用Gauss.Jordan消去法有 故解原方程的解为χ=(3-21)T。
故解原方程的解为χ=(3-21)T。
对方程组的增广矩阵[A,b,用Gauss.Jordan消去法有故解原方程的解为χ=(3,-2,1)T。
相似问题
常量组分的分析结果一般保留_________位有效数字 微量组分的分析结果_般保留_________
常量组分的分析结果一般保留_________位有效数字,微量组分的分析结果_般保留_____________位有效数字。各种误差与偏差一般要求保留___________位有效数
用幂法计算矩阵用幂法求下列矩阵按模最大的特征值和相应的特征向量。用幂法求下列矩阵按模最大的特征值和相
用幂法计算矩阵用幂法求下列矩阵按模最大的特征值和相应的特征向量。用幂法求下列矩阵按模最大的特征值和相应的特征向量。 请帮忙给出正确答案和分析,谢谢!
设f(χ)=sinχ g(χ)=cosχ χ∈[-1 1] 试用勒让德多项式分别对f(χ) g(χ)
设f(χ)=sinχ,g(χ)=cosχ,χ∈[-1,1],试用勒让德多项式分别对f(χ),g(χ)做最佳平方逼近三次和四次多项式,并估计误差。请帮忙给出正确答案和分析,谢谢!
已知函数y=(χ)过点(1 0) (2 -5) (3 -6) (4 3) 求经过这些点的Lagran
已知函数y=(χ)过点(1,0),(2,-5),(3,-6),(4,3),求经过这些点的Lagrange插值多项式L3(χ),并求f(第第一类Bessel函数y=f(χ)在χi(i=0,1,2
设A∈Rn×n为对称正定矩阵 χ∈Rn ‖χ‖=设矩阵 试求‖A‖1 ‖A‖∞ ‖A‖F。设矩阵 试
设A∈Rn×n为对称正定矩阵,χ∈Rn,‖χ‖=设矩阵 试求‖A‖1,‖A‖∞,‖A‖F。设矩阵 试求‖A‖1,‖A‖∞,‖A‖F。请帮忙给出正确答案和分析,谢谢!












